ReconstructLine - восстановление линий по точкам в QGIS
Обсудить в форуме Комментариев — 29Редактировать в вики
по адресу http://gis-lab.info/qa/reconstruct_line.html
Описание инструмента для создания линий по точкам в QGIS
ReconstructLine - это инструмент для интерактивного создания линейных объектов по точечным.
Вы наверняка сталкивались с инструментом, объединяющим точки в линии. Все такие инструменты работают либо последовательно, т.е. точки объединяются в линии так, как они идут в таблице, либо про атрибутам. Теперь представьте, что вам не важен порядок записей в таблице и атрибутивная информация отсутствует или бесполезна, но что вам все равно нужно объединить точки в линию.
Расширение ReconstructLine умеет восстанавливать линии по точкам, используя только их пространственное расположение. Расширение может работать в двух режимах, "восстанавливая" единую линию или несколько линий. Поскольку восстановление - это сложный алгоритм, ReconstructLine работает только интерактивно. Процесс восстановления может занять значительное время, если точек много.
ReconstructLine плохо подходит для облаков точек.
Реальный пример применения - у вас есть несколько треков снятых в разное время, возможно разными людьми и представляющих один и тот же линейный объект. Их все необходимо объединить в единый объект. Подобная задача часто возникает при съемке протяженных объектов - линий электропередач, трубопроводов и т.п.
| Создано в | Веб ГИС для вашей организации по доступной цене |
Замечания по установке[править]
Расширение доступно из официального репозитория.
ReconstructLine находится в разработке и протестирован с QGIS 2.6 и выше. Расширение работает в Windows и Linux (Ubuntu).
Исходный код модуля доступен в (репозитории на Github).
Алгоритм[править]
Модуль предназначен для работы с двумя типами расположения точек:
- Точки образуют единственную линию.
- Точки образуют несколько пересекающихся линий (основная линия и короткие боковые ответвления).
Для каждого из этих случаев точки обрабатываются отдельным алгоритмом. Пользователь может выбрать тот или иной алгоритм, нажав на соответсвующую точку на панели инструментов.
Случай одной линии[править]
При разработке модуля принималось во внимание то, что точки можно соединить между собой "логичным" образом, если они образуют "видимую глазами" кривую линию. В этом случае задачу можно сформулировать следующим образом:
- Дан набор точек .
- Дана метрика -- функция, которая измеряет расстояния между произвольной парой точек. Тогда потенциальной восстановленной кривой (т.е. последовательности точек ) можно поставить в соответствие её длину, равную сумме растояний между парами точек, составляющих восстановленную кривую: .
- Требуется найти среди всех комбинаций такую комбинацию, для которой ее длина L будет минимальной.
Нужно заметить, что требование того, что восстановленная кривая должна иметь минимальную длину из всех возможных комбинаций точек -- чисто эвристическое допущение, которое, тем не менее, хорошо согласуется с реальным положением дел. (Чтобы убедиться в этом достаточно нарисовать кривую, измерить ее длину, затем "перепутать" в ней пару или несколько пар точек и измерить длину новой кривой).
Приведенная выше формулировка задачи представляет собой хорошо известную задачу поиска Гамильтонова пути. Также хорошо известно, что эта задача уже при небольшом числе точек не может быть решена "в лоб" простым перебором вариантов, поскольку их число взрыовобразно растет. Так, например, для пяти точек будет всего 60 (т.е. 5!/2) возможных комбинаций, для десяти точек -- уже почти два миллиона, а, например, для тридцати -- количество комбинаций описывется числом, состоящим из 34-х цифр.
Поэтому алгоритмы построения Гамильтонова пути, используемые на практике, представляют собой субоптимальные алгоритмы, которые позволяют найти хорошее решение за приемлемое время, но не гарантируют того, что оно будет лучшим из всех возможных. В данном модуле в качестве основного алгорима использовались самоорганизующиеся карты Кохонена. Поскольку перед нами стоит задача восстановления линии, то и архитектура сети была выбрана линейной. Обученная сеть упорядочивает точки и в целом обеспечивает неплохой результат работы. Но в некоторых случаях "неудачного" расположения входных точек с одним узлом сети оказываются связаны несколько точек, их упорядоченность может оказаться нарушенной. Для того, чтобы отследить подобные случаи, в модуле используется постобработка: в упорядоченном картой Кохонена наборе точек производятся попарные перестановки соседних точек и измеряется совокупная длина линии. В итоге линия наименьшей длины возвращается в качестве результата алгоритма.
Случай линии с ответвлениями[править]
Бывает так, что точки образуют основную (длинную) линию, от которой отходят короткие боковые ходы. В этом случае предположение о том, что конечная линия должна представлять собой линию минимальной длины (Гамильтонов путь) не верно. Зато данный случах хорошо "ложится" на задачу о нахождении минимального остовного дерева.
В плагине реализуется классический алгоритм Прима, предназначенный для решения этой задачи. В отличие от предыдущего случая, строится не одна итоговая линия, а множество сегментов между соседними точками. В случае необходимости объединить сегменты в одну линию, пользователь может воспользоваться стандартным иструментом QGIS объединения геометрий.
Работа с расширением[править]
Режим одной линии[править]
После установки расширения появится новая панель инструментов с двумя кнопками: "копировать точки" и "вставить линию".
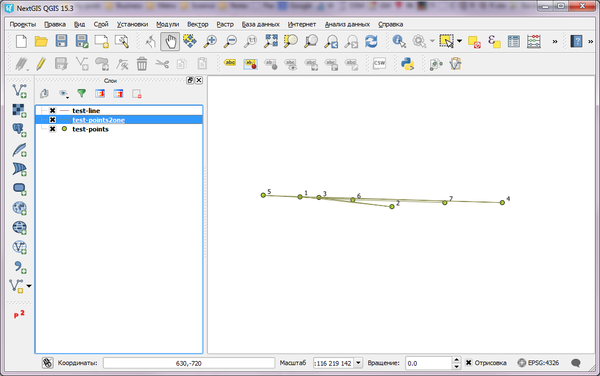
Предположим, что исходный набор точек выглядит следующим образом (обратите внимание на нумерацию, она отражает последовательность точек в таблице):
Что будет, если просто соединить их в линию (например с помощью расширения Points2One):
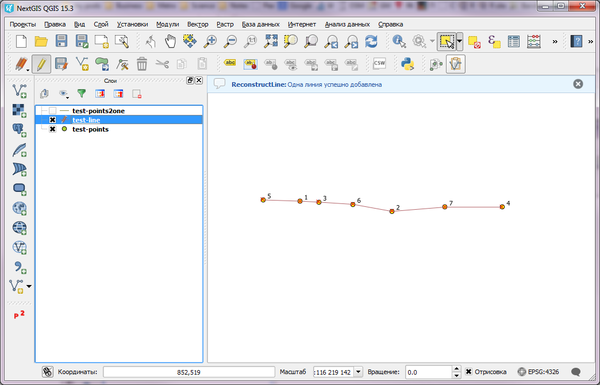
Для объединения с помощью ReconstructLine:
1. Инструментом выделения выделите нужные точки, нажмите на кнопку "Копировать точки" в панели инструментов ReconstructLine
2. Вставьте линию в линейный слой (если слоя нет - создайте новый или добавьте существующий). Выберите слой в списке слоёв, начните редактирование и нажмите на кнопку "Вставить линию" в панели инструментов ReconstructLine
Результат должен выглядеть более логично:
Режим восстановления нескольких линий[править]
Используя инструмент "вставить линии" можно попытаться реконструировать несколько линий в исходных данных. Особенностью работы данного алгоритма является то, что создается не одна, а много линий, по количеству сегментов соединяющих точки.
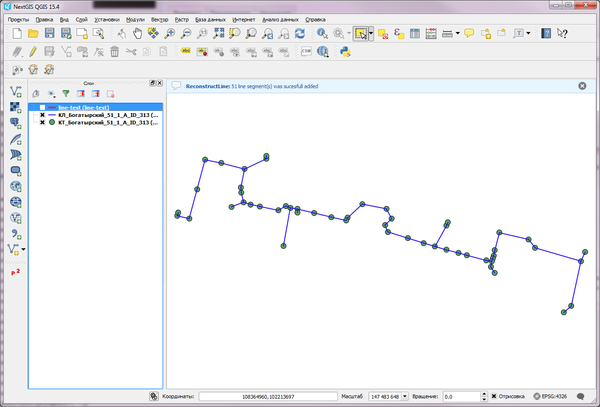
Для примера рассмотрим следующий набор данных:
Используя алгоритм восстановления линий можно достичь следующего результата:
Как можно видеть, автоматический алгоритм лишь в нескольких местах (синие фрагменты) не смог восстановить ожидаемую сеть.
Контакты[править]
Если вы нашли ошибку или у вас есть предложения по улучшению расширения — воспользуйтесь багтрекером. Кроме того, вопросы по использованию расширения можно задать авторам напрямую.
Ссылки по теме[править]
Обсудить в форуме Комментариев — 29Редактировать в вики
Последнее обновление: 2018-03-22 16:04
Дата создания: 27.04.2015
Автор(ы): Дмитрий Колесов
© GIS-Lab и авторы, 2002-2021. При использовании материалов сайта, ссылка на GIS-Lab и авторов обязательна. Содержание материалов - ответственность авторов. (подробнее).