Линейная засечка — это нахождение положения точки по координатам двух исходных пунктов и расстояниям от этих пунктов до определяемой точки.

Общие положения[править]

В качестве модели Земли принимается сфера с радиусом R, равным среднему радиусу земного эллипсоида. Аналогом прямой линии на плоскости является геодезическая линия на поверхности. На сфере геодезическая линия — дуга большого круга.

Введём следующие обозначения:

• φ — географическая широта,
• λ — географическая долгота,
• α — азимут дуги большого круга,
• σ — сферическое расстояние (длина дуги большого круга, выраженная в долях радиуса шара).

Линейное расстояние по дуге большого круга s связано со сферическим расстоянием σ формулой s = R σ.

Постановка задачи[править]

Исходные данные

координаты пунктов Q₁, Q₂ — φ₁, λ₁, φ₂, λ₂,

расстояния от пунктов Q₁, Q₂ до точки Q₃ — σ₁₃, σ₂₃.

Определяемые величины

координаты точки Q₃ — φ₃, λ₃.

Алгоритм[править]

Линейная засечка

Решение любого вида засечек сводится к нахождению полярных координат искомой точки, т.е. начального направления и расстояния на неё с одного из исходных пунктов. На конечном этапе координаты находятся из решения прямой геодезической задачи. Поскольку в линейной засечке расстояния σ₁₃ и σ₂₃ уже заданы, остаётся определить направление α₁₃ или α₂₃.

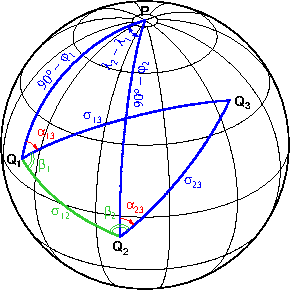
На рисунке синим цветом выделены заданные элементы сферических треугольников, красным цветом неизвестные, зелёным — вспомогательные элементы. Итак, в треугольнике Q₁Q₂Q₃ известны только два элемента — стороны σ₁₃ и σ₂₃. Из решения обратной геодезической задачи для пунктов Q₁, Q₂ можно получить недостающий третий элемент — расстояние σ₁₂, а также азимут α₁₂.

Последовательность действий:

1. решить обратную геодезическую задачу для Q₁, Q₂: по φ₁, λ₁, φ₂, λ₂ получить α₁₂, σ₁₂;
2. в треугольнике Q₁Q₂Q₃ по σ₁₂, σ₁₃, σ₂₃ вычислить угол β₁;
3. вычислить азимут α₁₃;
4. решить прямую геодезическую задачу для Q₁, Q₃: по φ₁, λ₁, α₁₃, σ₁₃ вычислить φ₃, λ₃.

Действия по первому и последнему пунктам рассмотрены в статьях Задачи на сфере: обратная геодезическая задача и Задачи на сфере: прямая геодезическая задача.

Угол β₁ и азимут α₁₃ вычисляются по формулам:

${\displaystyle {\begin{aligned}\cos \beta _{1}&={\dfrac {\cos \sigma _{23}-\cos \sigma _{12}\cos \sigma _{13}}{\sin \sigma _{12}\sin \sigma _{13}}}\\\alpha _{13}&=\alpha _{12}\mp \beta _{1}\end{aligned}}}$

Если величина косинуса превышает единицу, задача поставлена некорректно, не выполняется закон «Длина стороны не может превышать сумму длин других сторон».

В общем случае имеется два решения, расположенных симметрично относительно большого круга Q₁Q₂. Следует явно определить, с какой стороны от направления Q₁Q₂ находится точка Q₃: если слева, как на рисунке, то в последней формуле ставим знак минус, если же справа — знак плюс.

Пример программной реализации[править]

Пример функции SphereLinear на языке Си, реализующей вышеизоложенный алгоритм:

/*
 * Решение линейной засечки
 *
 * Аргументы исходные:
 *     pt1    - {широта, долгота} пункта Q1
 *     pt2    - {широта, долгота} пункта Q2
 *     dist13 - азимут направления Q1-Q3
 *     dist23 - азимут направления Q2-Q3
 *     clockwise - флаг направления:
 *                 0 - налево от линии Q1-Q2,
 *                 1 - направо от линии Q1-Q2
 *
 * Аргументы определяемые:
 *     pt3 - {широта, долгота} точки Q3
 */
int SphereLinear(double pt1[], double pt2[], double dist13, double dist23,
		 int right, double pt3[])
{
  double azi12, dist12, azi13;
  double cos_beta1;

  if (dist13 == 0.) {			      // Решение - точка Q1.
    pt3[0] = pt1[0];
    pt3[1] = pt1[1];
    return 0;
  } else if (dist23 == 0.) {		      // Решение - точка Q2.
    pt3[0] = pt2[0];
    pt3[1] = pt2[1];
    return 0;
  }

  SphereInverse(pt1, pt2, &azi12, &dist12);
  cos_beta1 = (cos(dist23) - cos(dist12) * cos(dist13))
    / (sin(dist12) * sin(dist13));
  if (fabs(cos_beta1) > 1.)		      // Решение не существует.
    return -1;
  azi13 = clockwise ? azi12 + acos(cos_beta1) : azi12 - acos(cos_beta1);
  SphereDirect(pt1, azi13, dist13, pt3);

  return 0;
}

Этот код находится в архиве Sph.zip в файле sph.c. Кроме того, в файл sph.h включены следующие определения:

#define A_E 6371.0				// радиус Земли в километрах
#define Degrees(x) (x * 57.29577951308232)	// радианы -> градусы
#define Radians(x) (x / 57.29577951308232)	// градусы -> радианы

Теперь напишем программу, которая обращается к функции SphereLinear для решения линейной засечки:

#include <stdio.h>
#include <stdlib.h>
#include "sph.h"

int main(int argc, char *argv[])
{
  char buf[1024];
  double pt1[2], pt2[2], pt3[2];
  double lat1, lon1, lat2, lon2, dist13, dist23;
  int clockwise;

  while (fgets(buf, 1024, stdin) != NULL) {
    sscanf(buf, "%lf %lf %lf %lf %lf %lf %d",
	   &lat1, &lon1, &lat2, &lon2, &dist13, &dist23, &clockwise);
    pt1[0] = Radians(lat1);
    pt1[1] = Radians(lon1);
    pt2[0] = Radians(lat2);
    pt2[1] = Radians(lon2);
    if (SphereLinear(pt1, pt2, dist13 / A_E, dist23 / A_E, clockwise, pt3))
      puts("\t"); /* Решений нет */
    else
      printf("%f\t%f\n", Degrees(pt3[0]), Degrees(pt3[1]));
  }
  return 0;
}

В архиве Sph.zip этот код находится в файле lin.c. Создадим исполняемый модуль lin компилятором gcc:

$ gcc -o lin lin.c sph.c -lm

Впрочем, в архиве есть Makefile. Для MS Windows готовую программу lin.exe можно найти в архиве Sph-win32.zip.

Программа читает данные из стандартного ввода консоли и отправляет результаты на стандартный вывод. Для чтения и записи файлов используются символы перенаправления потока «>» и «<» соответственно. Из каждой строки ввода программа считывает координаты первого и второго пунктов φ₁, λ₁, φ₂, λ₂ в градусах, расстояния σ₁₃ и σ₂₃ в километрах (точнее, в единицах константы A_E) и признак направления (0 — налево от линии Q₁Q₂, 1 — направо); решает линейную засечку; выводит в строку вывода координаты третьей точки φ₃, λ₃ в градусах.

Создадим файл lin.dat, содержащий одну строку данных:

30 0 60 30 5001.1309 1722.9431 1

После запуска программы

$ lin < lin.dat

получим φ₃, λ₃:

52.000001 54.000000

В архиве Sph-py.zip находится код на языке Питон. Выполнение скрипта в командной консоли:

$ python lin.py lin.dat

Ссылки[править]

• Вычисление расстояния и начального азимута между двумя точками на сфере
• Вычисление угла образованного тремя точками на сфере
• Задачи на сфере: обратная геодезическая задача
• Задачи на сфере: прямая геодезическая задача
• Задачи на сфере: угловая засечка
• Краткий справочник по сферической тригонометрии
• Earth radius
• Степанов Н. Н. Сферическая тригонометрия