Адаптивное сглаживание для шумных ЦМР
Обсудить в форуме Комментариев — 8Редактировать в вики
по адресу http://gis-lab.info/qa/adaptive-smooth-dem.html
Описание метода сглаживания и устранения шума для ЦМР - перевод статьи
Adaptive smoothing for noisy DEMs
John Gallant, CSIRO Land and Water, Canberra, ACT, Australia, 2011
Оригинал статьи: http://gis-lab.info/docs/gallant2011_adaptive_smoothing_for_noisy_dems.pdf
Краткое содержание[править]
ЦМР, полученные с помощью дистанционного зондирования, включая лидарные и радарные ЦМР, обеспечивают лучшую детализацию поверхности, чем традиционные интерполированные ЦМР, но страдают от случайных шумов, которые искажают измерения таких форм поверхности, как склоны и направления потоков. Сглаживание - это эффективный метод снижения шума, но он так же, как правило, влияет на важные особенности рельефа, понижение на холмах, повышение во впадинах и стирает важные мелкие детали. Эта статья описывает подход многомасштабного адаптивного сглаживания, который реагирует как на уровень рельефа, так и на уровень шума в ЦМР, активно сглаживая места, где величина зашумленности превышают значения высот местности, сглаживая немного или не сглаживая вовсе места, где шум меньше, чем значения рельефа. Данный метод прост и эффективен и может быть легко реализован в среде растровой ГИС. Он демонстрируется на зашумлённых данных SRTM.
Введение[править]
Цифровая модель рельефа (ЦМР) - это несовершенное представление реальной земной поверхности. Влияние дефектов ЦМР на геоморфометрические операции зависит от того, как эти дефекты воздействуют на измерение таких форм поверхностей как склоны, направления потоков и кривизну. В годы становления компьютеризированной геоморфометрии, или цифрового изучения местности, большинство ЦМР создавались путем интерполяции относительно редких источников данных, главным образом, полученных с топографических карт. Такие ЦМР достаточно сглаженные, а их главным изъяном является недостаточная детализация рельефа, особенно на участках с пологим рельефом, где горизонтали расположены далеко друг от друга. В последнее время многие ЦМР изготавливаются с помощью радарных и лидарных данных дистанционного зондирования или фотограмметрическими способами. Эти ЦМР имеют минимум одно измеренное значение для каждой ячейки сетки, поэтому хорошо передают характер поверхности, но измерения обычно подвержены ошибкам. Это проявляется в виде шумовых значений в данных о высотах с различными особенностями в зависимости от источника данных. Измерения небольших локальных форм рельефа значительно подвержены влиянию случайных шумов и, как правило, существует больше проблем на участках с простым рельефом, где нет выраженных форм рельефа. Сглаживание путем локального усреднения - это эффективная операция для снижения шума, но она ведет к замене истинных значений высот, и реальный рельеф местности не сохраняется: высокий уровень сглаживания хорошо удаляет шум, но, как правило, уничтожает небольшие формы рельефа и скругляет резкие границы, в то время как низкий уровень сохраняет особенности рельефа, но не эффективно удаляет шум. В идеале метод сглаживания должен сглаживать сильнее там, где уровень шума больше по отношению к перепаду высот, и меньше или совсем не сглаживать там, где шум значительно меньше перепада высот. Различные соотношения сигнал/шум могут быть следствием изменений уровня значимого сигнала (топографические изменения), так и изменения уровня шума. Эта статья описывает такой метод адаптивного сглаживания, который удаляет шум, при этом сохраняя особенности рельефа, реагирует на изменения уровня шума, а так же может заполнить недостающие данные. Он использует статистический подход с мульти-разрешением, который является весьма эффективным и может быть легко реализован в среде растровой ГИС.
Метод адаптивного сглаживания[править]
Метод адаптивного сглаживания основан на идеях Ли (Lee)[1], но расширен до мульти-разрешения. Метод Ли рассчитывает окрестное среднее арифметическое Z_{ij} и дисперсию с поправкой на шум Q_{ij} в точке (i, j), а затем получает вычисленное значение, как взвешенную сумму среднего и исходного зашумленного значения:
(1)
где σ21 это дисперсия шума; xi,j - истинное значение в точке i, j и zi,j - это значение, поврежденное шумом. Суть в том, что там где дисперсия зашумленного сигнала значительно больше, чем шум, зашумленное значение используется в качестве предполагаемой истинной величины, так как шум не оказывает большого влияния; там, где дисперсия мала по сравнению с шумом, используется окрестное среднее арифметическое, значительно устраняющее шум. Метод Ли был использован для сглаживания ЦМР, например, Симардом (Simard) и др. [2], который использовал фильтр типа Ли размерами 5х5 для сглаживания высот SRTM c постоянным стандартным отклонением шума в 1.8 м Ли отмечает, что "Использование различных размеров области расчета значительно влияет на качество обработки изображений. Если область слишком мала, алгоритм фильтрации шума не эффективен. Если область слишком велика, мелкие детали изображения будут потеряны в процессе фильтрации." Решение по выбору размера области расчета в данном методе адаптивного сглаживания заключается в том, что нужно сглаживать с помощью областей различных размеров, позволяя дисперсии в области каждого размера контролировать, на сколько среднее арифметическое в данной области влияет на вычисленное значение. Алгоритм учитывает различную дисперсию шума в пространстве и рассчитывает средние арифметические значения и дисперсии во вложенных областях так, что все расчеты после этапа с начальным разрешением производятся по сеткам с постепенно увеличиваемым размером ячейки, что ведет к весьма эффективной обработке. Алгоритм мульти-разрешений похож на мульти-масштабный метод сглаживания Калмана (Kalman) [3,4] и состоит из ряда последовательных обобщений с последующим рядом уточнений до исходного разрешения. исходные значения алгоритма:
(2)
за исключением мест, где нет данных, для которых исходные значения:
(3)
w это вес для каждой ячейки, равный обратной дисперсии V, а n это количество ячеек с данными. Затем, для каждого шага i от 1 до imax:
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
На каждом шаге веса и квадраты весов суммируются (4), (5) и рассчитывается взвешенное среднее арифметическое дисперсии(6). Дисперсия для группы точек с данными vg - это сумма (9) межгрупповой дисперсии vbg (7) и внутригрупповой дисперсии vwg (8). Межгрупповая дисперсия - это дисперсия, обусловленная различиями между групповыми средними, а внутригрупповая дисперсия обусловлена различиями между значениями внутри группы, так же как и при дисперсионном анализе. Дисперсия средних значений vm эквивалентна обратному суммарному весу (10). Эффективное количество ячеек neff получено из весов (12); оно равно количеству ячеек n когда все веса равны, но оно меньше n когда веса неравны. Среднее значение дисперсии шума mv получено из количества ячеек и суммарного веса (13). Последний этап (14) сравнивает групповую дисперсию со средней дисперсией шума и использует статистическую проверку для принятия решения, достаточно ли мала групповая дисперсия, чтобы значения внутри группы могли считаться равными среднему значению, в этом случае берется дисперсия среднего как дисперсия для данного разрешения; иначе, берется групповая дисперсия. Критическое значение ![]() вычисляется со степенями свободы равными количеству эффективных ячеек neff уменьшенному на единицу.
вычисляется со степенями свободы равными количеству эффективных ячеек neff уменьшенному на единицу.
Это дает вложенные последовательности средних значений и дисперсий при постепенно более грубых разрешениях, которые могут быть объединены в обратную последовательность. Этот процесс начинается с:
(15)
Затем, для каждого шага i от imax до 1:
(16)
(17)
(18)
Сглаженные в грубом масштабе высоты zs и дисперсии vs сначала улучшаются до следующего более высокого разрешения (16), дисперсия, рассчитанная путем объединения в этом разрешении, и сглаженная дисперсия из более грубого разрешения совмещаются (17) для создания сглаженной дисперсии в более высоком разрешении, чем сглаженная высота, полученная из взвешенной суммы (18) высоты в этом разрешении и сглаженной высоты в более грубом разрешении. Конечный результат это z0s , сглаженная ЦМР, и Vs0 - предполагаемая дисперсия. Каждый шаг алгоритма соответствует относительно простому вычислению растра, которое может быть реализовано в ГИС. Используя ArcInfo GRID, суммы на первом этапе можно рассчитывать с помощью функции AGGREGATE для групп ячеек размерами 3х3, а уточнения во втором этапе можно рассчитать с помощью функции FOCALMEAN, после того как соответственно установлены интервалы и размеры ячеек. В результатах присутствует некоторое количество незначительных артефактов, которые можно устранить, используя более сложный этап улучшения. Метод воспринимает расположенный по нормальному закону и пространственно нерегулярный шум; степень влияния отклонения размещения шума от идеальных условий на качество сглаживания пока не исследована. Статистическая проверка (14) - это, вероятно, главная отличительная черта данного алгоритма. Она выражает предположение, что на участках, где сгруппированная дисперсия достаточно мала, измеренные высоты следует считать подверженными случайным погрешностям в измерениях единственного истинного значения, т.е. то, что земная поверхность на данной территории плоская. Тогда дисперсия для этой группы (для того, чтобы объединить значения на стадии улучшения) - это дисперсия рассчитанного среднего vm , которое гораздо меньше, чем дисперсия измерений. Такая небольшая дисперсия гарантирует, что среднее играет решающее значение для выборок, так как в (17).
Оценка шума на ЦМР[править]
Для применения данного алгоритма адаптивного сглаживания к данным ЦМР, необходима оценка дисперсии для каждой точки. Описанный здесь способ оценки шума был разработан для использования с односекундными данными SRTM (после устранения полос, заполнения пробелов и удаления влияния растительности, Gallant et al. [5]) и требовал некоторой дополнительной подстройки к особенностям данной ЦМР, в частности к пространственно обусловленной природе шума. Для других источников данных может потребоваться другой способ; в некоторых случаях оценка шума может быть выполнена в процессе создания ЦМР.
Для каждой ячейки среднее значение рассчитывается по кольцевой области радиусом от 3 до 5 ячеек; кольцо означает, что значения, окружающие целевую ячейку не учитываются при расчете среднего значения. Рассчитывается разность между целевой ячейкой и средним значением, а затем получают стандартное отклонение этой разности по области из 5 ячеек. Это даёт информацию о величине дисперсии высот относительно средних высот на небольшом расстоянии - идея в том, что эта дисперсия должна быть наиболее зашумленной, так как небольшая топографическая дисперсия произведет пространственно связанные отличия от среднего значения, которое не сильно повлияет на стандартные отклонения разностей.
Эта первоначальная оценка величины шума всё еще весьма приблизительна, поэтому она сглаживается двумя этапами медианной фильтрации, сначала группировкой по прямоугольнику размерами 5х5, а затем по круговой области радиусом в 5 ячеек по полученной более грубой сетке. Результирующая сетка затем улучшается до начального разрешения ЦМР с помощью билинейного пересчета. Оценка соответствует стандартному отклонению шума. Рис. 1 показывает результат этого анализа по односекундной ЦМР SRTM на часть западной Австралии, где уровни шума очень различны.
Заметьте, что этот метод эффективно отличает шум от рельефа местности в равнинных областях с пологими склонами, но не способен определить различие в областях с более выраженным рельефом или там, где присутствуют резко выраженные формы рельефа в равнинных областях. Подход, выбранный для решения данной проблемы, состоял в последовательном снижении предполагаемого уровня шума, как стандартного отклонения высоты, увеличенной на 5 метров.
Рис.1 Предполагаемое стандартное отклонение шума для данных SRTM, западная Австралия 119.0E 33.6S. Квадрат - область покрытая деревьями с более высокой отражающей способностью и, следовательно, меньшим уровнем шума, чем на окружающей очищенной территории.
Адаптивное сглаживание SRTM[править]
Рис. 2 показывает отмывку рельефа, а рис. 3 показывает уклон, рассчитанный по односекундной ЦМР SRTM до и после применения адаптивного метода сглаживания с использованием оценки шума, показанной на рисунке 1. Изображение отмывки рельефа подчеркивает плавность областей с пологим рельефом после адаптивного сглаживания. Пологие склоны около 1-2%, которые преобладают в данном ландшафте, подавлены шумом до сглаживания. После сглаживания они совершенно очевидны. Более крутые склоны в юго-восточном углу изображения в значительной степени не затронуты сглаживанием.

Рис. 2. Отмывка рельефа на участке территории с рисунков 1 и 3, полученная из данных SRTM до (слева) и после (справа) адаптивного сглаживания.
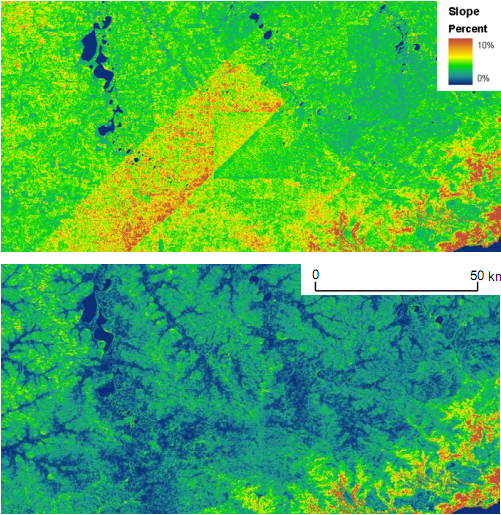
Рис.3 Уклоны, полученные из односекундных данных SRTM до (сверху) и после (снизу) адаптивного сглаживания с использованием стандартного отклонения шума с рисунка 1.
Заключение[править]
Этот относительно простой алгоритм адаптивного сглаживания эффективно устраняет пространственно распределенный шум в ЦМР, полученных с помощью данных дистанционного зондирования. Способ был так же успешно применен к лидарным ЦМР с использованием постоянного стандартного отклонения шума в 0.2 м. Алгоритм сглаживания к тому же заполняет участки с отсутствующими данными сглаженными соседними значениями, благодаря применению нулевых весов в (3), которые могут быть использованы как простой метод для заполнения пустот.
Литература[править]
[1] Lee, J.-S., 1980. “Digital image enhancement and noise filtering by
use of local statistics.” IEEE Transactions on Pattern Analysis and Machine
Intelligence, PAMI-2, 165-168
[2] Simard, M., K. Zhang, V. H. Rivera-Monroy, M. S. Ross, P. L. Ruiz,
E. Castaneda-Moya, R. R. Twilly, and E. Rodríguez, 2006. Mapping height
and biomass of mangrove forests in Everglades National Park with SRTM
elevation data, Photogrammetric Engineering and Remote Sensing, 72(3),
299-311.
[3] Fieguth, P.W., W.C. Karl, A.S. Willsky, & C. Wunsch, 1995.
“Multiresolution optimal interpolation and statistical analysis of
TOPEX/POSEIDON satellite altimetry”. IEEE Transactions on Geoscience
and Remote Sensing, 33, 280-292
[4] Slatton, K.C., M.M. Crawford and B.L. Evans, 2001. “Fusing
interferometric radar and laser altimeter data to estimate surface
topography and vegetation heights.” IEEE Transactions on Geoscience and
Remote Sensing, 39, 2470-2482
[5] Gallant, J.C., T.I. Dowling, A.M. Read, N. Wilson, P. Tickle (2010)
1 Second SRTM Level 2 Derived Digital Elevation Model v1.0.
http://www.ga.gov.au/meta/ANZCW0703013355.html, last accessed 15
May 2011
Обсудить в форуме Комментариев — 8Редактировать в вики
Последнее обновление: 2016-10-25 12:19
Дата создания: 18.04.2012
Автор(ы): Андрей Кушкин
© GIS-Lab и авторы, 2002-2021. При использовании материалов сайта, ссылка на GIS-Lab и авторов обязательна. Содержание материалов - ответственность авторов. (подробнее).























