• Главная
• Вопросы и ответы

Вычисление угла образованного тремя точками на сфере

Немного геометрии для решения задачи нахождения угла для случая сферы, используемый код может применяться в других расширениях.

Обсудить в форуме Комментариев — 10

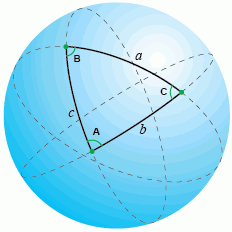
Согласно сферической теореме косинусов: косинус одной стороны сферического треугольника равняется произведению косинусов двух других его сторон плюс произведение синусов тех же сторон на косинус угла между ними.

Одно из отличий сферического треугольника от обычного заключается в том, что сумма его углов больше 180 градусов.

В уравнениях используются угловые длины в радианах.

Отсюда, зная координаты трех точек и вычислив расстояния между ними по формулам вычисления расстояний на сфере, можно получить любой из трех углов, например угол A:

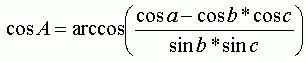
Скачать пример расчета в Excel

Вычислениям приведенным выше соответствует следующий код на языке Avenue (координаты трех точек и расчеты расстояний передаются отдельно) (скачать скрипт):

'вычисление расстояний по формулам большого круга,
'GreatCirclesDist - название скрипта для вычислений
'расстояний по формулам большого круга в проекте
pnts = {}
pnts = pnts.add(a)
pnts = pnts.add(b)
ab = av.run("GreatCirclesDist", pnts).Get(0)
pnts = {}
pnts = pnts.add(b)
pnts = pnts.add(c)
bc = av.run("GreatCirclesDist", pnts).Get(0)
pnts = {}
pnts = pnts.add(a)
pnts = pnts.add(c)
ca = av.run("GreatCirclesDist", pnts).Get(0)
A = (((a.cos) - (b.cos*c.cos))/b.sin*c.sin).ACos.AsDegrees

Обсудить в форуме Комментариев — 10

Последнее обновление: September 09 2021

Дата создания: 06.06.2006
Автор(ы): Максим Дубинин