Уменьшение количества узлов линий.

Инструмент для уменьшения количества точек в линейных слоях по алгоритму Дугласа-Пойкера (Douglas-Peuker), с настраиваемым уровнем детализации.

Замечания по установке[править]

Расширение доступно из официального репозитория.

DPSimplify разработан для QGIS версии 1.0.0 и старше, для работы не требует наличия дополнительных модулей.

Исходный код модуля можно получить выполнив команду

svn co http://svn.gis-lab.info/dpsimplify dpsimplify

Работа с расширением[править]

После подключения и запуска расширения с помощью кнопки

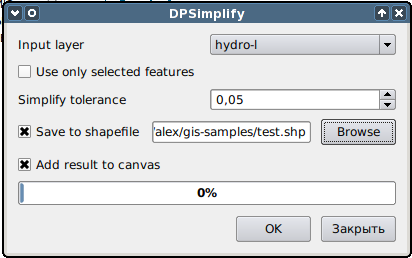
расширения появится окно:

Исходный слой выбирается из выпадающего списка. Можно обрабатывать весь слой или только выделенные объекты. Если установлен флаг «Save to shapefile» — результат упрощения будет записан в указанный файл, в противном случае будут изменены объекты исходного слоя. При работе со слоем есть возможность отменить операцию упрощения, но следует иметь в виду, что отмена производится для всех объектов. Порог упрощения задается в единицах карты (метры или градусы).

По окончанию процесса появляется окно с информацией о количестве узлов в рабочем наборе до и после упрощения. Если результат не устраивает, то можно, не закрывая окно расширения, выполнить откат, задать другое значение порога и запустить обработку заново.

Пример упрощения с помощью DPSimplify (зеленая линия с красными узлами — исходная, синяя — конечная, порог 500 м)

Контакты[править]

Если вы нашли ошибку или у вас есть предложения по улучшению расширения — воспользуйтесь багтрекером.

Ссылки по теме[править]

• Установка модулей расширения в QGIS
• Документация по QGIS