• Главная
• Вопросы и ответы

Полиномиальные преобразования - математика для большого количества точек

Математические выкладки решения задачи, применяемой при привязке данных

Введение

При операции географической привязки данных, то есть перевода данных из локальной системы координат в географическую или прямоугольную, сам пересчет обычно происходит "за сценой" и его особенности часто понятны пользователю только интуитивно. Эта статья показывает полный алгоритм пересчета и может быть использована для реализации алгоритмов привязки данных в своем ПО и просто для более полного понимания того, что происходит на самом деле. Для менее насыщенного формулами описания рекомендуем ознакомиться со статьей "Полиномиальные преобразования". Указанная статья, хотя и содержит формулы преобразований, не показывает детальной их реализации, однако представляет важную информацию о применении данных преобразований на практике. Для того, чтобы посмотреть примеры реализации подобных преобразований, рекомендуем ознакомиться со статьей "Полиномиальные преобразования - примеры реализации для большого количества точек", которая показывает примеры реализации на языке R и Excel.

Так как одно из наиболее часто используемых преобразований при привязки - полиномиальное преобразование 2-й степени, мы иллюстрируем наши расчеты на его примере. Вычисления для аффинного преобразования (оно же полиномиальное преобразование 1-й степени) выполняются аналогичным образом, с меньшим количеством коэффициентов.

Данная статья иллюстрирует случай, когда количество точек привязки больше минимально необходимого (n = 6). В случае если равно точек 6 следует ознакомиться со отдельными статьями (математика, примеры реализации).

Математика

Решение задачи трансформации сводится к нахождению коэффициентов системы уравнений. Напомним, что в случае полиномиального преобразования 2-й степени, система уравнений выглядит следующим образом:

где:

x,y - координаты в исходной системе координат (известны)
x^',y^' - координаты в конечной системе координат (известны)
a_0-5,b_0-5 - коэффициенты (неизвестны)

Таким образом, имея 12 неизвестных, нам понадобится минимум 6 пар точек с известными координатами до и после трансформации (x1,y1; x2,y2; x3,y3; x4,y4; x5,y5; x6,y6 и x1',y1'; x2',y2'; x3',y3'; x4',y4'; x5',y5'; x6',y6'), но обычно используется большее число точек (x1,y1 ... xn,yn), что делает возможным вычисление ошибки, здесь рассматривается именно этот случай:

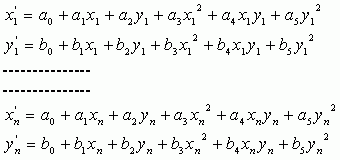
Или, перегруппируя этот набор уравнений по x и y:

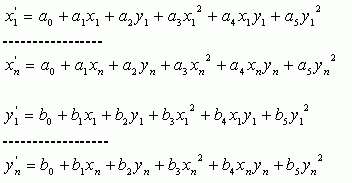
Каждая группа используется соответственно для получения коэффициентов a_i и b_i. Точек в этом случае больше, но условие возможности умножения матриц, согласно которому умножение возможно если количество колонок в левой матрице равно количеству рядов в правой - сохраняется. Поэтому рядов в основной матрице (и соответственно точек привязки) может быть сколько угодно. В матричной форме это выглядит следующим образом, для a и b:

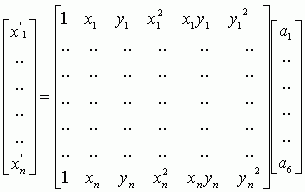
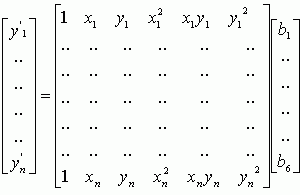
В случае минимально необходимого количества точек, основная матрица Х является квадратной и ее можно инвертировать, для получение коэффициентов, каждая часть уравнения должна быть умножена на обратную матрицу с коэффициентами, например для коэффициентов a:

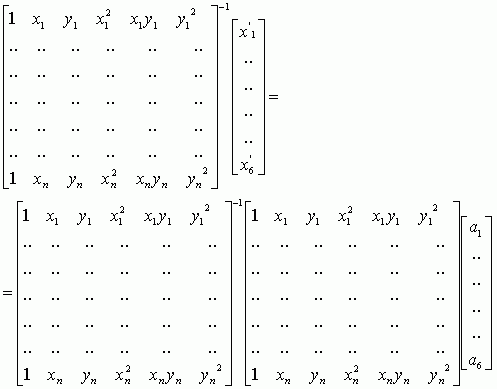
В случае когда n>7, основная матрица не квадратная и подобное решение уже не подходит, так как ее нельзя инвертировать.

Не вдаваясь в подробности его вывода, решение такой системы в матричной форме будет выглядеть следующим образом:

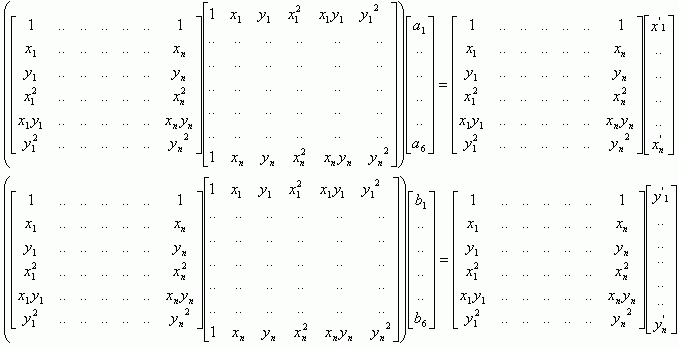
Или в упрощенной нотации:

Умножив правую и левую часть на инвертированный продукт умножения, получим матричную форму уравнения для вычисления коэффициентов, так же известную как метод наименьших квадратов:

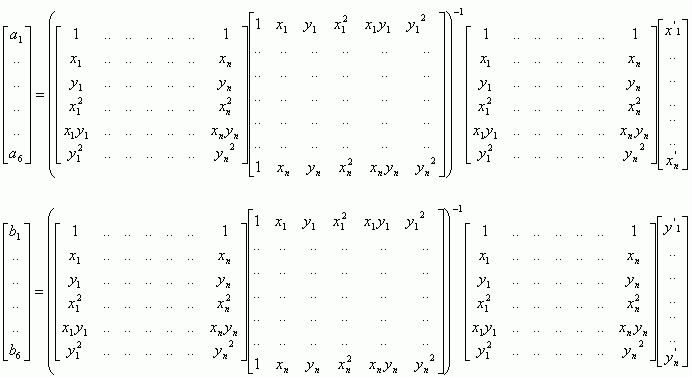
Или в упрощенной нотации:

Таким образом, для решения данной системы, наше программное обеспечение должно уметь производить операции получения обратной матрицы, транспонирование и умножения матриц.

Полученный набор коэффициентов подставляется потом в исходные уравнения и задача получения новых координат решается для каждого пиксела исходного растра, получая таким образом результат в выходной системе координат.

Обсудить в форуме Комментариев — 16

Последнее обновление: September 09 2021