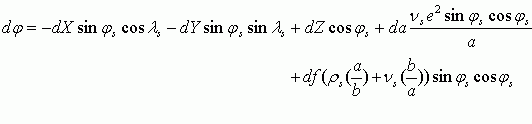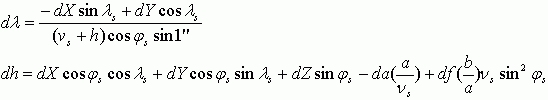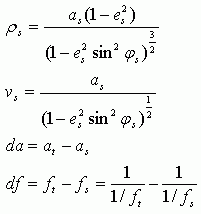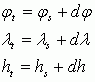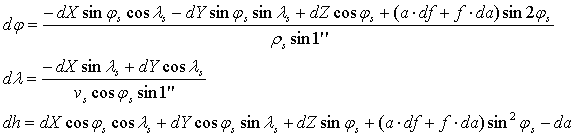Методы трансформации с формулами

Координаты любой точки земной поверхности в разных системах координат будут различаться, переход от одной системы координат к другой осуществляется с помощью специальных формул преобразований и набора параметров, используемых в этих формулах.

Преобразования из геоцентрических в геоцентрические координаты[править]

Эти преобразования могут использоваться как посредник между преобразованием из географических в географические координаты по схеме:

географические в геоцентрические > геоцентрические в геоцентрические > геоцентрические в географические

Geocentric translations[править]

EPSG code: 9603

Параметры: смещение по оси X, смещение по оси Y, смещение по оси Z

Если исходная и конечная система координат геоцентрические, оси эллипсоидов параллельны, главный меридиан - Гринвичский и нет разницы в масштабах, это преобразование позволяется вычислить координаты в конечной системе координат простым прибавлением смещения соответствующим координатам в исходной системе координат.

Xt = Xs + dX
Yt = Ys + dY
Zt = Zs + dZ

Position Vector[править]

EPSG code: 9606

Параметры: смещение по оси X, смещение по оси Y, смещение по оси Z, поворот по оси X, поворот по оси Y, поворот по оси Z, масштабирование

Одно из 7-параметрических преобразований Гельмерта, использующее формулу Бурша-Вольфа.

${\displaystyle {\begin{pmatrix}X_{t}\\Y_{t}\\Z_{t}\end{pmatrix}}=M{\begin{pmatrix}1&-R_{z}&+R_{y}\\+R_{z}&1&-R_{x}\\-R_{y}&+R_{x}&1\end{pmatrix}}{\begin{pmatrix}X_{s}\\Y_{s}\\Z_{s}\end{pmatrix}}+{\begin{pmatrix}dX\\dY\\dZ\end{pmatrix}}}$

где

X_s, Y_s, Z_s- координаты точки в исходной системе координат.

X_t, Y_t, Z_t- координаты точки в конечной системе координат.

dX, dY, dZ - вектор смещения, добавляемый к исходной точке, также является координатами начала координат исходной системы координат в конечной системе координат.

Rx, Ry, Rz - повороты, добавляемые к вектору смещения. Положительное значение означает поворот по часовой стрелке исходя из начала координат вдоль положительного хода соответствующей оси. Углы измеряются в радианах.

M - масштабирование вектора преобразования в исходной системе координат необходимое, чтобы получить правильный масштаб в конечной системе. M = 1+dS*10^-6, где dS - масштабирование выражаемое в частях на миллион.

Это преобразование может использоваться как промежуточное между преобразованием из географических в географические координаты (см. Geocentric translations).

Пример программной реализации можно посмотреть здесь.

Coordinate frame rotation[править]

EPSG code: 9607

Параметры: смещение по оси X, смещение по оси Y, смещение по оси Z, поворот по оси X, поворот по оси Y, поворот по оси Z, масштабирование.

Одно из 7-параметрических преобразований Гельмерта, использующее формулу Бурша-Вольфа.

${\displaystyle {\begin{pmatrix}X_{t}\\Y_{t}\\Z_{t}\end{pmatrix}}=M{\begin{pmatrix}1&+R_{z}&-R_{y}\\-R_{z}&1&+R_{x}\\+R_{y}&-R_{x}&1\end{pmatrix}}{\begin{pmatrix}X_{s}\\Y_{s}\\Z_{s}\end{pmatrix}}+{\begin{pmatrix}dX\\dY\\dZ\end{pmatrix}}}$

Преобразование аналогичное Position Vector, но отличающееся инвертированными значениями поворотов Rx, Ry, Rz. Международная геодезическая ассоциация (IAG) и международный стандарт ISO 19111 (Geographic information -- Spatial referencing by coordinates) рекомендуют для описания преобразования использовать Position Vector. В ArcGIS это преобразование эквивалентно преобразованию Бурша-Вольфа.

Это преобразование может использоваться как посредник между преобразованием из географических в географические координаты (см. Geocentric translations).

Преобразования из географических в географические координаты[править]

Данный вид преобразований позволяет перейти от географических координат к географическим сразу, без этапа пересчета из одной геоцентрической системы координат в другую. Параметры перехода из геоцентрической в геоцентрическую СК используются как часть общего набора параметров.

Преобразование Молоденского[править]

EPSG code: 9604

Параметры: смещение по оси X, смещение по оси Y, смещение по оси Z, разница в длине малой полуоси, разница в уплощении

где:

φ, λ - разница по широте и долготе в угловых секундах;
dX, dY, dZ - параметры геоцентрического смещения
ρ - горизонтальный (меридиональный) радиус кривизны на данной широте первого эллипсоида
ν - вертикальный (широтный) радиус кривизны на данной широте первого эллипсоида
da - разница между длинами малых полуосей (a1 - a2) исходного и конечного эллипсоидов
df - разница между уплощениями этих эллипсоидов.

где

f - уплощение эллипсоида;
e - эксцентриситет;

Сокращенное преобразование Молоденского[править]

EPSG code: 9605

смещение по оси X, смещение по оси Y, смещение по оси Z, разница в длине малой полуоси, разница в уплощении

This transformation is a truncated Taylor series expansion of a transformation between two geographic coordinate systems, modelled as a set of geocentric translations.

где φ_s,t - исходная и конечная долгота, λ_s,t - исходная и конечная широта, h_s,t - исходная и конечная высота:

где:

φ, λ - разница по широте и долготе в угловых секундах;
dX, dY, dZ - параметры геоцентрического смещения;
ρ - горизонтальный (меридиональный) радиус кривизны на данной широте первого эллипсоида;
ν - вертикальный (широтный) радиус кривизны на данной широте первого эллипсоида;
da - разница между длинами малых полуосей (a1 - a2) исходного и конечного эллипсоидов;
df - разница между уплощениями этих эллипсоидов.

где

f - уплощение эллипсоида;
e - эксцентриситет;

Сокращенная (abridged) форма преобразования Молоденского отличается от полной тем, что она игнорирует сдвиг по высотеи используется для сокращения вычислений.

Ссылки по теме[править]

• Загрузка данных с GPS в нужной системе координат (DNRGarmin)
• ГОСТ 51794-2001 Аппаратура радионавигационная глобальной навигационной спутниковой системы и глобальной системы позиционирования. Системы координат. Методы преобразования координат определяемых точек.
• Формулы пересчета данных GPS-измерений из WGS-84 в СК-42 и обратно
• NGA: Standard Molodensky Transformations