Форумы GIS-Lab.info

Здравствуйте!
У меня путаница с проекциями случилась.
Есть геометрия (для наглядности - круглые полигоны) в системе координат "WGS 84 / Pseudo Mercator" (Рис. 1).

: Рис. 1; Буфер.png (30.16 КБ) 12441 просмотр

"Преобразую на лету" свои полигоны в WGS84 - получаю растянутые круги (рис. 2).

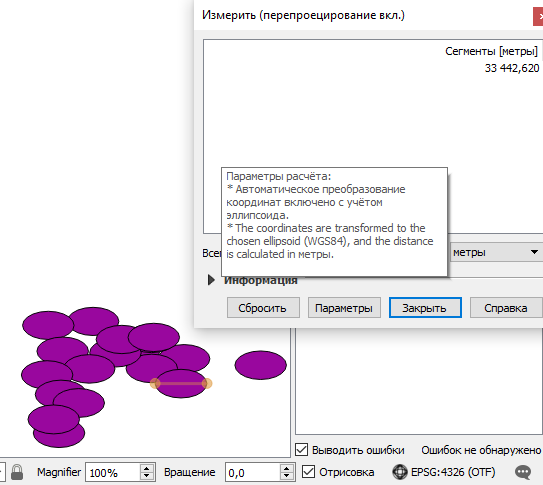
: Рис. 2; Конвертирую.png (31.21 КБ) 12441 просмотр

Смотрю в гугле на проекцию Меркатора - и вижу равномерно растянутые круги (по X и Y) от экватора на север и на юг -> делаю вывод: мои круги то должны быть, судя по проекции, равномерно изменены, а они не равномерно изменены. Вопрос возникает: с чем это связано? Наверное с тем, что в гугле схема преобразований с глобуса (длина экватора равна длине нулевого меридиана) на плоскость, думаю? Смотрю в параметры СК - и вижу, что A=B=6378137 (большая полуось равна малой ), значит в QGISe так же - с глобуса на плоскость...Отсюда вопрос: Как так то?! )

Дальше делаю замеры линейкой (инструментом "измерить линию" в QGIS) диаметра круга - получаю по X и Y одинаковые значения (в моём случае 33 км). Ну вроде норм.

Дальше делаю всё наоборот т.е. беру те же круги, но в проекции WGS84 и "преобразовываю на лету" в "WGS 84 / Pseudo Mercator". Получаю круги, которые теперь уже сжаты. Думаю - "ну всё норм"... начинаю проводить измерения диаметра линейкой (той же),а измерения показывают, что значения не равны (X=33,337 км, а Y=60 км) (Рис. 3).

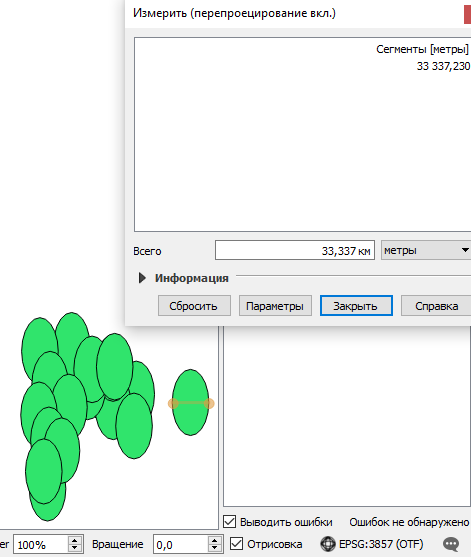
: Рис. 3; обратно.png (26.81 КБ) 12441 просмотр

Тут возник опять вопрос - "как так то!?"...
Объясните пожалуйста почему так происходит? и с чем это связано? А именно:
1) почему, приобразуя в одну сторон, измерения по X/Y равны, при изменившейся геометрии, а в другую сторону измерения не равны.
2) Почему форма кругляшков не соответствует тому что по ссылке в гугл? Вроде бы - что то Меркатор, что это...

Та картинка условная, показывает увеличение площади. Меркатор сохраняет подобие углов, а размеры искажает с севера на юг, идеально только на экваторе. И в QGIS вы видите всё правильно, круг в меркаторе на местности будет овалом.

Чтобы увидеть равномерно меняющийся масштаб или другую форму искажения масштаба, нужно круги создавать в проекции, которая имеет минимальные искажения масштаба - UTM, например. А потом уже перепроецировать их в Меркатор, псевдо-Меркатор или географическую проекцию.
А вы делаете какую-то ерунду - создаете круги в уже искаженной проекции Меркатора или географической.

В продолжение темы)
Когда открываю карту OSM в QGIS'е, в системе координат карты OSM (тот же epsg:3857 Mercator), провожу измерения по карте, то получаю изменения в размерах (относительно WGS84 конечно же) не пропорциональные тем, которые получаю при измерениях радиуса своих кругов.
Так например возьмём расстояние от Томска до Мельниково - примерно 56 км, затем измерим этот же отрезок в Меркаторе - получаем примерно 99 км. Т.е. значение увеличилось примерно в 1.8 раз (тут всё ясно).

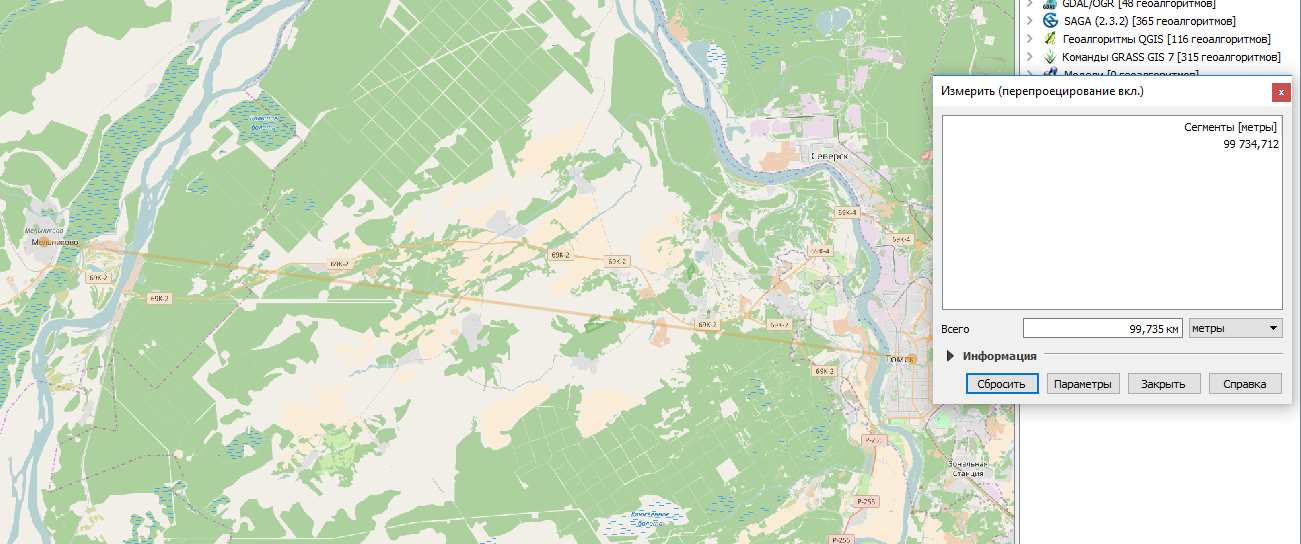
: Рис. 1; Расстояние.PNG (268.12 КБ) 12347 просмотров

Поскольку измерения провожу примерно вдоль долготы, то этот наверно тоже самое, что и измерения диаметра круга по оси X (вдоль долготы). Если взять пример с кругами - результат противоположный. Круги уменьшают свой диаметр при переводе из wgs84 в Mercator с тем же коэффициентом. В данном примере почему нету пропорциональности? Карта OSM'а строилась в каком то другом Меркаторе? Наставьте меня на путь истинный, в чем я заблуждаюсь? ))

А кто вам сказал, что искажение измерений пропорциональны? Особенно в ПсевдоМеркаторе, который не равноугольный.

Совершенно не понял вопрос, но многие, как и вы , путают проекцию на эллипсоид или шар с самим эллипсоидом. Невозможно "перевести из WGS84 в Mercator" только потому, что WGS84 это эллипсоид, а Mercator это проекция на какой-либо эллипсоид или шар. Посмотрите внимательно в QGIS: раздел "Географические системы координат" +proj=longlat на эллипсоиде +datum=WGS84. Т.е. проекция - географическая или широта-долгота.
В прямоугольных системах координат параметров обычно пишут побольше. Если вы на них посмотрите, то ваши вопросы с отображением должны отпасть сами собой.

Вот для размышлений картинка с видом глобуса. Красная линия — точки на расстоянии 100 км от центра на эллипсоиде WGS 84, зелёная — «круг», построенный в географической системе координат, синие линии — 100-км буферы в проекциях World Mercator и Pseudo Mercator. На картинке они сливаются в одну линию, как и должно быть.

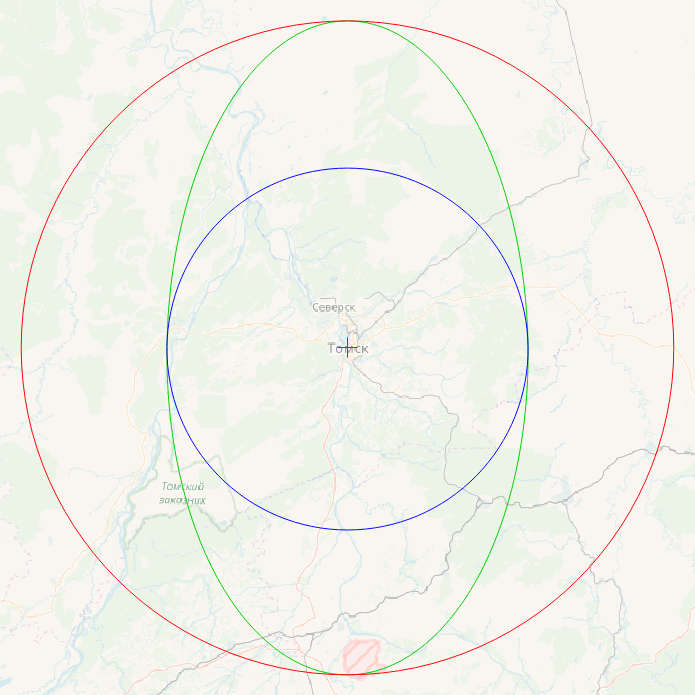
: img_20170914_201633.png (69.75 КБ) 12312 просмотров

Позволю себе цитату с главной страницы данного сайта:

Для поиска ответа на свой вопрос начните с раздела Статьи

И cамая первая статья в разделе «Координаты и проекции» Часто задаваемые вопросы по координатам, проекциям, системам координат содержит ответы на все Ваши вопросы.

Andrey Zhukov писал(а): ↑
14 сен 2017, 14:28
Особенно в ПсевдоМеркаторе, который не равноугольный

Pseudo Mercator — это проекция Меркатора на сфере. Старина Герхард Меркатор создал эту проекцию именно для сферы, а на эллипсоид её натянули много позже. Проекция Меркатора — короткое имя конформной цилиндрической проекции. Она по определению является равноугольной при отображении любой поверхности, будь то сфера, трёхосный эллипсоид, геоид, груша или чемодан.

Спойлер

Может, Вы намекаете, что Земля не является сферой? Так она и эллипсоидом вращения не является! При описании земной поверхности нет принципиальной разницы между такими абстракциями, как эллипсоид с нулевым сжатием и эллипсоид со сжатием 1/300. Второй ближе к истине, но не истина. Попытки отказывать проекциям на сфере в полноценности нелепы.

Игорь Белов писал(а): ↑
14 сен 2017, 21:03
содержит ответы на все Ваши вопросы.

Видимо я очень плохо задаю вопросы...

Игорь Белов писал(а): ↑
14 сен 2017, 21:03
зелёная — «круг», построенный в географической системе координат

Зелёный круг (овал) вроде бы в Меркаторе построен. Нет?

Andrey Zhukov писал(а): ↑
14 сен 2017, 14:28
А кто вам сказал, что искажение измерений пропорциональны?

Ну происходит же переход, из одной системы координат в другую, одинаковый (из epsg 4326 в epsg в 3857)... Так? Что в случае с картой OSM, что в случае с моими кругами (Так?). Если смотреть на изображение от Игоря Белова - Карта OSM (её геометрия) не изменяется в след за изменением геометрии от красного круга (от WGS84) до зелёного круга (до Меркатора). Т.е. карта, должна же тоже сжиматься как и красный круг, а она не сжимается; но ведь карта OSM выполнена в той же СК что и круг: epsg:3857. Карта как бы отображается в WGS84 а измерения по ней идут в Меркаторе. Вот что терзает моё недоумение...

Вместо слов.

На сколько я понимаю, от топикстартера ускользает концепция построения окружностей в единицах проекции, которые совпадают с "реальными" метрами только на экваторе или которые там им поставлены в соответствие.

t[0]p писал(а): ↑
12 сен 2017, 10:10
Есть геометрия (для наглядности - круглые полигоны) в системе координат "WGS 84 / Pseudo Mercator" (Рис. 1).

t[0]p писал(а): ↑
12 сен 2017, 10:10
"Преобразую на лету" свои полигоны в WGS84 - получаю растянутые круги (рис. 2).

Логично, ведь географические системы координат QGIS показывает как цилиндрическую равнопромежуточную проекцию (в которой координаты на плоскости численно равны или пропорциональны географическим). Это не равноугольная проекция. Меридианы в ней отображаются параллельными линиями, в то время как на глобусе они сходятся к полюсам.

t[0]p писал(а): ↑
12 сен 2017, 10:10
Дальше делаю всё наоборот т.е. беру те же круги, но в проекции WGS84 и "преобразовываю на лету" в "WGS 84 / Pseudo Mercator". Получаю круги, которые теперь уже сжаты. Думаю - "ну всё норм"... начинаю проводить измерения диаметра линейкой (той же),а измерения показывают, что значения не равны (X=33,337 км, а Y=60 км) (Рис. 3).

t[0]p писал(а): ↑
12 сен 2017, 10:10
делаю вывод: мои круги то должны быть, судя по проекции, равномерно изменены, а они не равномерно изменены.

Те "круги", которые вы нарисовали в системе координат "долгота/широта", вовсе не будут окружностями на глобусе - это ведь не декартова система координат. А значит, не будут ими и в проекции Меркатора. Она сохраняет форму небольших объектов, но делает это по отношению к поверхности отображаемого сфероида.

Я бы посоветовал нарисовать координатную сетку меридианов и параллелей и экспериментировать с ней - так вам будет понятнее, что происходит при перепроецировании.

Игорь Белов писал(а): ↑
14 сен 2017, 21:03
Проекция Меркатора — короткое имя конформной цилиндрической проекции. Она по определению является равноугольной при отображении любой поверхности, будь то сфера, трёхосный эллипсоид, геоид, груша или чемодан.

Но ведь это неправда. Вы не сможете конформно изобразить чемодан на плоскости, пользуясь формулами проекции Меркатора или геометрическими построениями с использованием цилиндра.

Проекция - это отображение одной поверхности на другую, и свойства её, включая равноугольность, зависят не только от формул проекции, но и от геометрических свойств поверхности, а также от системы координат, с помощью которой мы задаём точки на этой поверхности. Формулы проекции Меркатора на сфере в общем случае не обеспечивают равноугольности при отображении эллипсоида вращения с их помощью, если мы используем геодезическую широту. Для этого есть проекция Меркатора на эллипсоиде. И математически равноугольность проекции нужно рассматривать, сравнивая углы в проекции с углами на эллипсоиде, на котором она основана.

Проекция EPSG:3857 основана на эллипсоиде WGS84, несмотря на то, что использует формулы для сферы. Если мы используем "честную" проекцию Меркатора на сфере, то порядок преобразований из WGS84 в координаты проекции такой:
1. Преобразуем геодезическую широту на эллипсоиде WGS84 в широту на сфере (для сферы геодезическая широта совпадает с геоцентрической).
2. Подставляем полученную широту и долготу в формулы проекции Меркатора для сферы. Эта проекция равноугольна по отношению к поверхности сферы.
Для EPSG:3857 первый шаг пропускается, то есть геодезическая широта на эллипсоиде WGS84 непосредственно подставляется в формулы сферической проекции Меркатора. Проекция не является равноугольной относительно поверхности эллипсоида, а поверхность сферы в этом случае вообще не имеет отношения к нашим координатам, заданным на эллипсоиде. В proj.4 пропуск первого шага реализуется через грязный хак с добавлением параметра

Код: Выделить всё

+nadgrids=@null

к определению проекции.

Я согласен с тем, что, поскольку Земля не является ни сферой, ни эллипсоидом, небольшие отклонения свойств проекции Pseudo Mercator от настоящей проекции Меркатора (на сфере или эллипсоиде) не являются практически значимыми в большинстве применений.

Ariki писал(а): ↑
18 сен 2017, 13:54
Вы не сможете конформно изобразить чемодан на плоскости, пользуясь формулами проекции Меркатора или геометрическими построениями с использованием цилиндра.

Удивительная наивность! Что же мне помешает? Некоторые ограничения имеются: выпуклость, непрерывность, гладкость и др. Если пухлый чемодан с закруглёнными углами им удовлетворяет, его поверхность безусловно может быть отображена на плоскость в конформной цилиндрической проекции. Разумеется, формулы, использовавшиеся для эллипсоида, должны быть заменены на другой алгоритм, соответствующий поверхности чемодана.

Ariki писал(а): ↑
18 сен 2017, 13:54
Проекция EPSG:3857 основана на эллипсоиде WGS84, несмотря на то, что использует формулы для сферы.

То есть, проекция EPSG:3857 основана на сфере.

Весь остальной бред сводится к мистической вере в то, что конформная проекция на сфере обязана быть конформной по отношению к эллипсоиду.

Игорь Белов писал(а): ↑
18 сен 2017, 15:17
Что же мне помешает? Некоторые ограничения имеются: выпуклость, непрерывность, гладкость и др. Если пухлый чемодан с закруглёнными углами им удовлетворяет, его поверхность безусловно может быть отображена на плоскость в конформной цилиндрической проекции. Разумеется, формулы, использовавшиеся для эллипсоида, должны быть заменены на другой алгоритм, соответствующий поверхности чемодана.

В том-то и дело, что нам нужен или круглый чемодан, или некруговой цилиндр, или выпуклая груша, или негеодезическая широта, или вообще другие формулы. Почему при таких допущениях конформное отображение (если оно вообще существует в случае чемодана) должно называться цилиндрической проекцией Меркатора - мне непонятно.

Игорь Белов писал(а): ↑
18 сен 2017, 15:17
То есть, проекция EPSG:3857 основана на сфере.

Весь остальной бред сводится к мистической вере в то, что конформная проекция на сфере обязана быть конформной по отношению к эллипсоиду.

Потому что в случае Pseudo Mercator у нас нет широты точки местности на сфере, но есть широта на эллипсоиде.

Я рассматриваю проекцию как чёрный ящик, трансформирующий геодезические координаты на некотором заданном эллипсоиде в декартовы координаты на плоскости. Когда я говорю "основана на эллипсоиде WGS84", я имею в виду, что на вход ей подаются геодезические широта и долгота на эллипсоиде WGS84, как это и происходит в веб-картографии, где эта проекция появилась и применяется. То, что внутри этого чёрного ящика используется радиус некоей сферы, мне как пользователю проекции неинтересно. А вот то, что проекция искажает углы по сравнению с углами на моём эллипсоиде, - достаточно важно. И никакой мистической веры в этом нет, это практически значимый факт, о котором должен быть осведомлён любой разработчик веб-ГИС.

Псевдо-Меркатором такое геометрически бессмысленное использование формул сферической проекции Меркатора тоже впервые назвал не я, потому что надо же как-то отличать это от правильного использования. Если мы пересчитываем координаты между двумя проекционными системами координат, базирующимися на разных эллипсоидах, мы в качестве одного из этапов пересчитываем геодезические координаты с одного эллипсоида на другой (обычно через декартовы геоцентрические). Для широты это необходимо, даже если начало отсчёта и направления осей геоцентрических систем совпадают. Я не вижу причин, почему мы не должны этого делать в случае, если один из эллипсоидов - сфера. Web Mercator - это результат исторического недоразумения, случившегося, когда инженеры Google Maps из соображений вычислительной эффективности или по незнанию пренебрегли этим шагом.

Немножко ссылок:
PROJ.4 FAQ
Web Mercator: Non-Conformal, Non-Mercator
Implications of WebMercator and Its Use in Online Mapping

Ariki писал(а): ↑
18 сен 2017, 17:32
Потому что в случае Pseudo Mercator у нас нет широты точки местности на сфере, но есть широта на эллипсоиде.

Про отношение местности к какому-бы то ни было эллипсоиду мы говорили. Давайте начнём отсюда, поскольку это, похоже, первый пункт среди суеверий и предрассудков: «Псевдо Меркатор использует в качестве широты геодезическую широту эллипсоида, а так делать неправильно». Итак, позвольте задать простую задачу.

Задача №1

Дано. Две поверхности относимости — сфера и эллипсоид вращения — совмещены главными осями.

Вопрос. Будут ли параллельны друг другу нормали к поверхности сферы и эллипсоида, восстановленные в точках с одинаковой геодезической широтой на одноимённых меридианах?

Разрешаю пользоваться учебниками.

Форумы GIS-Lab.info

Из Меркатора в WGS84 и обратно.

Из Меркатора в WGS84 и обратно.

Re: Из Меркатора в WGS84 и обратно.

Re: Из Меркатора в WGS84 и обратно.

Re: Из Меркатора в WGS84 и обратно.

Re: Из Меркатора в WGS84 и обратно.

Re: Из Меркатора в WGS84 и обратно.

Re: Из Меркатора в WGS84 и обратно.

Re: Из Меркатора в WGS84 и обратно.

Re: Из Меркатора в WGS84 и обратно.

Re: Из Меркатора в WGS84 и обратно.

Re: Из Меркатора в WGS84 и обратно.

Re: Из Меркатора в WGS84 и обратно.

Re: Из Меркатора в WGS84 и обратно.

Re: Из Меркатора в WGS84 и обратно.

Re: Из Меркатора в WGS84 и обратно.