Геометрия: проверка пересечения треугольника и окружности
-
Shasoft
- Интересующийся
- Сообщения: 37
- Зарегистрирован: 24 июл 2009, 14:47
- Репутация: 0
Геометрия: проверка пересечения треугольника и окружности
Требуется определить факт пересечения треугольника (заданным тремя точками ) и окружности (заданной центром и радиусом). Проблема в том, что точки задаются широтой и долготой и обычные алгоритмы из 2D геометрии не подходят.
Может кто-нибудь может подсказать куда смотреть для решения проблемы? Или даст ссылку на готовые формулы?
Может кто-нибудь может подсказать куда смотреть для решения проблемы? Или даст ссылку на готовые формулы?
- Дмитрий Барышников
- Гуру
- Сообщения: 2572
- Зарегистрирован: 17 ноя 2009, 19:17
- Репутация: 261
- Откуда: Москва
Re: Геометрия: проверка пересечения треугольника и окружности
Я бы преобразовал окружность в набор точек с определенной дисретизацией. А дальше обычный случай сравнения двух полигонов (Алгоритмы Вейлера-Азертона, Сазерленда-Ходгмана, Кируса-Бека и др.).
-
Shasoft
- Интересующийся
- Сообщения: 37
- Зарегистрирован: 24 июл 2009, 14:47
- Репутация: 0
Re: Геометрия: проверка пересечения треугольника и окружности
Алгоритм предполагается использовать в 3D карте для отсечения невидимых тайлов, так что желательно минимум вычислений.
Сейчас исследую возможность определения пересечений с представлением сторон треугольника окружностями.
Сейчас исследую возможность определения пересечений с представлением сторон треугольника окружностями.
- Дмитрий Барышников
- Гуру
- Сообщения: 2572
- Зарегистрирован: 17 ноя 2009, 19:17
- Репутация: 261
- Откуда: Москва
Re: Геометрия: проверка пересечения треугольника и окружности
Естественно вначале необходимо тупо проверить экстенты исходных фигур (что очень быстро). Еще можно квадратичное дерево построить, есть реализации трехмерных деревьев (http://www2.research.att.com/~marioh/spatialindex/).
Это как? Может вершин? Все равно вершины треугольника не показатель. Они могут и не попадать в окружность, а сторона может попадать.Shasoft писал(а): Сейчас исследую возможность определения пересечений с представлением сторон треугольника окружностями.
-
Shasoft
- Интересующийся
- Сообщения: 37
- Зарегистрирован: 24 июл 2009, 14:47
- Репутация: 0
Re: Геометрия: проверка пересечения треугольника и окружности
Перед тем как делать проверку: проверяю пересекаются ли окружность пересечение с которой нужно проверить и окружность, описанная вокруг треугольника. Если НЕ пересекаются, то значит пересечение нет. Если пересекаются, то только тогда работаю по описанному ниже алгоритму.
Треугольник в сферических координатах можно представить вот так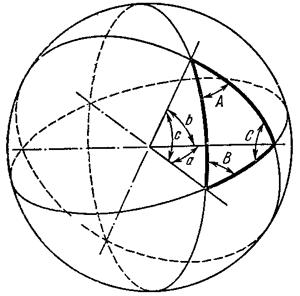
т.е. в виде треугольника на сфере. Каждую сторону такого треугольника на сфере можно рассматривать как часть окружности, проходящей через центр. Каждую такую окружность можно представить двумя параметрами:
1) Координаты центра окружности на поверхности сферы
2) радиусом (в радианах) этой сферы.
И тогда нам нужно вычислить
Тогда если L<(R-r), то окружность не пересекает треугольник
R-радиус окружности, задающей сторону треугольника
L - расстояние от центра окружности задающей сторону до центра окружности пересечение с которой требуется определить
r - радиус окружности, пересечение с которой требуется проверить
Если ни одна из трех проверок не выявило НЕПЕРЕСЕЧЕНИЯ, то значит пересечение ЕСТЬ.
Треугольник в сферических координатах можно представить вот так
т.е. в виде треугольника на сфере. Каждую сторону такого треугольника на сфере можно рассматривать как часть окружности, проходящей через центр. Каждую такую окружность можно представить двумя параметрами:
1) Координаты центра окружности на поверхности сферы
2) радиусом (в радианах) этой сферы.
И тогда нам нужно вычислить
Тогда если L<(R-r), то окружность не пересекает треугольник
R-радиус окружности, задающей сторону треугольника
L - расстояние от центра окружности задающей сторону до центра окружности пересечение с которой требуется определить
r - радиус окружности, пересечение с которой требуется проверить
Если ни одна из трех проверок не выявило НЕПЕРЕСЕЧЕНИЯ, то значит пересечение ЕСТЬ.
- Дмитрий Барышников
- Гуру
- Сообщения: 2572
- Зарегистрирован: 17 ноя 2009, 19:17
- Репутация: 261
- Откуда: Москва
Re: Геометрия: проверка пересечения треугольника и окружности
Непонятно где на вашей сфере находится проверяемая окружность. Как ее плоскость пересекает сферу?
-
Shasoft
- Интересующийся
- Сообщения: 37
- Зарегистрирован: 24 июл 2009, 14:47
- Репутация: 0
Re: Геометрия: проверка пересечения треугольника и окружности
Проверяемой окружности на сфере нет. Картинку не я рисовал, просто (на мой взгляд )данный рисунок наглядно демонстрирует, как можно представить стороны треугольника на сфере в виде окружностей.
Плоскость проверяемой окружности НЕ пересекает сферу, она находится на самой сфере.
Плоскость проверяемой окружности НЕ пересекает сферу, она находится на самой сфере.
- Дмитрий Барышников
- Гуру
- Сообщения: 2572
- Зарегистрирован: 17 ноя 2009, 19:17
- Репутация: 261
- Откуда: Москва
Re: Геометрия: проверка пересечения треугольника и окружности
Если и окружность и треугольник находятся на сфере (!), то возвращаемся к варианту 1 - viewtopic.php?f=25&t=5327#p25911
Просто сферические координаты (широта и долгота) представляются как Y и Х соответственно. Единственное, надо пересчитать радиус из метров (километров и т.п.) в градусы.
Просто сферические координаты (широта и долгота) представляются как Y и Х соответственно. Единственное, надо пересчитать радиус из метров (километров и т.п.) в градусы.
-
Shasoft
- Интересующийся
- Сообщения: 37
- Зарегистрирован: 24 июл 2009, 14:47
- Репутация: 0
Re: Геометрия: проверка пересечения треугольника и окружности
Я сначала тоже думал, что обычные 2D методы помогут, как только я представлю широту и долготу как x и y.
Однако это не так именно из-за того, что щирота и долгота - это координаты на СФЕРЕ.
Т.е. значение lng=-180 и lng=180 для сферических координат означают одно и тоже, а вот для 2D это уже не так. Именно поэтому 2D геометрия не прокатывает.
Однако это не так именно из-за того, что щирота и долгота - это координаты на СФЕРЕ.
Т.е. значение lng=-180 и lng=180 для сферических координат означают одно и тоже, а вот для 2D это уже не так. Именно поэтому 2D геометрия не прокатывает.
- Дмитрий Барышников
- Гуру
- Сообщения: 2572
- Зарегистрирован: 17 ноя 2009, 19:17
- Репутация: 261
- Откуда: Москва
Re: Геометрия: проверка пересечения треугольника и окружности
Прокатывает! Так все ГИС работают и Гугл тоже. Надо просто ограничения учитывать в крайних точках (например, если будет переход от 179 к -179, то надо рассматривать участок от 179 до 181).
-
Shasoft
- Интересующийся
- Сообщения: 37
- Зарегистрирован: 24 июл 2009, 14:47
- Репутация: 0
Re: Геометрия: проверка пересечения треугольника и окружности
Я тоже такой вариант рассматривал. Но потом запутался и решил спросить на этом форуме. 
Я запутался с lat коордлинатой, каким образом её корректировать, а тут как раз наткнулся на рисунок, приведенный выше и мысль потекла в другом направлении.
P.S. А радиус у меня и так уже в радианах. Координаты тоже в радианах, так как переход от радиан к градусом простой, а в расчетах везде нужны значения в радианах.
Я запутался с lat коордлинатой, каким образом её корректировать, а тут как раз наткнулся на рисунок, приведенный выше и мысль потекла в другом направлении.
P.S. А радиус у меня и так уже в радианах. Координаты тоже в радианах, так как переход от радиан к градусом простой, а в расчетах везде нужны значения в радианах.
Кто сейчас на конференции
Сейчас этот форум просматривают: Semrush [Bot] и 5 гостей