Полиномиальные преобразования
Формулы и примеры расчетов полиномиальных преобразований
Обсудить в форуме Комментариев — 0
Формулы полиноминальных преобразований используются для перевода исходных координат (обычно локальных-прямоугольных) в конечные (обычно спроектированные - прямоугольные). В зависимости от искажения изображения, количества контрольных точек (GCP – ground control point), и их размещения относительно друг друга, для выражения необходимого преобразования могут потребоваться достаточно сложные полиноминальные формулы. Сложность полинома выражается через его порядок. Порядок – это показатель наивысшей степени, используемой в полиноме.
Линейные преобразования
Преобразование 1-го порядка – линейное преобразование. Это преобразование может изменять:
- положение по X и/или Y; Изменение положения, смещает изображение на определенное число пикселей по X и Y.
- масштаб по X и/или Y; Коэффициенты масштабирования по X и Y могут быть различными
- наклон по X и/или Y;
- поворот; При повороте, можно определить любое положительное или отрицательное число градусов, для поворота по- и против часовой стрелки соответственно. Поворот происходит вокруг центрального пикселя изображения.
- Отражение; слева направо, сверху вниз, сверху вниз и слева направо (аналогично повороту на 180 градусов)
Преобразование 1-го порядка может быть использовано для перевода исходного (например только что отсканированного) изображения в прямоугольную систему координат, преобразования одной прямоугольной системы координат в другую, обычно это преобразование используется для относительной небольших фрагментов.
Примерами применения этого преобразования могут быть: исправление перекосов в данных дистанционного зондирования, поворота отсканированных топографических листов, и поворота данных с нисходящих орбит так, что бы север был вверху изображения (а не по ходу орбиты).
Преобразование 1-го порядка также может быть использовано для данных, которые уже спроецированы на плоскость. Например, часто данные дистанционного зондирования, уже находятся в локальной прямоугольной системе координат, но не приведены к соответствующей проекции. При использовании данного типа преобразования, не имеет смысла увеличение порядка преобразования, если при первом порядке возникает большая среднеквадратическая ошибка. Сначала, необходимо проверить другие возможные источники ошибок: качество опорных точек, их распределение и другие возможные систематические ошибки.
На рисунке показано, как изменяются данные при линейных преобразованиях.

Для осуществления полиномиального преобразования первой степени необходимо найти 6 коэффициентов - по три на каждую координату (X и Y): a0, a1, a2, b0, b1, b2. Эти коэффициенты, далее используются в собственно уравнениях полиномиального преобразования первой степени (эквивалентного также аффинному преобразованию):
x0 = a0 + a1x + a2y
y0 = b0 + b1x + b2y
где x,y - исходные координаты, x0,y0 - конечные координаты
Нелинейные преобразования
Нелинейные преобразования – это преобразования 2-го и более порядка. Эти преобразования могут корректировать нелинейные искажения. На рисунке изображены примеры результатов некоторых нелинейных преобразований.

Преобразования 2-го порядка могут быть использованы для преобразования данных в географической системе координат (широта, долгота) в прямоугольную, для преобразования данных больших областей (для учета кривизны Земли), для точно привязки искаженных по той или иной причине данных (например, из-за искажений линз камеры, плохо отсканированных материалов) и т.д.
Матрица преобразования
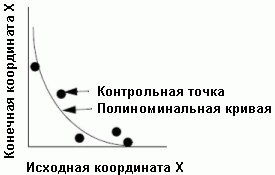
Матрица преобразования рассчитывается по контрольным точкам. Матрица состоит из коэффициентов, которые используются в формулах полиномов для преобразования координат. Размерность матрицы зависит от порядка используемого преобразования. Коэффициенты матрицы преобразований рассчитываются таким образом, чтобы получить формулы полиномиального преобразования с как можно меньшей ошибкой перевода исходных координат в конечные. Получить коэффициенты, которые не приводят к ошибкам удается не всегда. Пример, иллюстрирующий ошибку исходной координаты относительно конечной и кривой, аппроксимирующей зависимость между ними, выраженной полиномом (не все точки лежат на линии, расстояние от исходной точки до кривой полинома - среднеквадратичная ошибка). Для простоты в примере показано только отношение исходной и конечной координаты X и описывающее его кривая, в реальной жизни, исходных координат 2 и конечных координат 2, поэтому зависимость между ними аппроксимируется не кривой, а плоскостью.
Количество коэффициентов матрицы преобразований для преобразования порядка t равно:
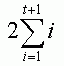
Это число необходимо умножить на 2 – для двух наборов коэффициентов, один - для X, другой для Y. Более простая формула для получения количества коэффициентов:
![]()
Очевидно, что размерность матрицы преобразований увеличивается с ростом порядка преобразования, соответственно минимальное количество контрольных точек необходимых для вычислений коэффициентов матрицы тоже растет.
Каждая контрольная точка влияет на расчетные коэффициенты, если нет идеального соответствия каждой контрольной точки полиному, который представлен этими коэффициентами. Расстояние между кривой и расчетной координаты точки – называется ошибкой RMS (среднеквадратической ошибкой точки). Для расчета матрицы преобразований по набору контрольных точек используется метод среднеквадратической регрессии (метод наименьших квадратов) на основе контрольных точек расставляемых пользователем от исходного (привязываемого) материала, к конечному материалу (тому, к которому привязывают).
Формула вычисления полинома порядка t
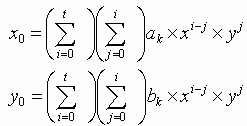
Где: t – порядок полинома, ak и bk – коэффициенты, индекс k для ak и bk вычисляется как:

Например, для преобразования 3-го порядка будет использоваться 20 коэффициентов:
![]()
Формула для преобразования 3-го порядка, после вычисления коэффициентов, может выглядеть так:
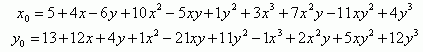
Влияние порядка преобразования
Расчет формул полиномов высоких порядков и выходных значений сложнее, чем расчет полиномов первых порядков. Поэтому, полиномы высоких порядков применяются для изображений требующих для привязки более сложных искажений. Для понимания влияния различных порядков преобразования при спрямлении изображения, полезно рассмотреть выходные величины полиномов различных порядков.
В следующем примере, для просты, используется только одна координата (X), вместо двух (X, Y), которые для расчетов в полиномиальных преобразованиях. Это позволяет использовать двухмерные графики, иллюстрирующие, как использование преобразования определенного порядка позволяет связать исходные и конечные координаты. Из-за того, что в примере используется только координата X, число используемых контрольных точек меньше реально требуемого для преобразований соответствующих порядков.
Коэффициенты, подобные тем, которые использованы в примере, обычно рассчитываются по методу наименьших квадратов. Предположим, что введены следующие контрольные точки:
Исходная координата X |
Конечная координата X |
|---|---|
1 |
17 |
2 |
9 |
3 |
1 |
Эти точки позволяют выполнить преобразование 1-го порядка для координат X, которые удовлетворяют следующему уравнению (коэффициенты указаны в скобках):
![]()
Где: xr = конечная координата X, xi = исходная координата X
В данном случае, уравнение принимает такую же форму, как и уравнение линии (y = b + mx), отсюда и линейность преобразования.

Однако, что произойдет, если вторую контрольную точку изменить следующим образом?
Исходная координата X |
Конечная координата X |
|---|---|
1 |
17 |
2 |
7 |
3 |
1 |
Эти точки нельзя соединить одной прямой линией, что означает, что они не могут быть описаны посредством полинома 1-го порядка, так как было описано выше.

В данном случае, эти точки выражаются через полином 2-го порядка:
![]()
Полиномы 2-го порядка и выше – нелинейные.

Что если добавить еще одну контрольную точку?
Исходная координата X |
Конечная координата X |
|---|---|
1 |
17 |
2 |
7 |
3 |
1 |
4 |
5 |

Как видно на рисунке, четвертая точка не лежит на кривой, выраженной уравнением полинома 2-го порядка. Для того, чтобы все точки лежали на кривой, порядок преобразования должен быть увеличен до 3-х. Результирующее уравнение и кривая изображены на рисунке.

Рисунок иллюстрирует преобразование 3-го порядка. Однако, возможно, это уравнение излишне усложнено. Выполнение преобразования координат с использованием этого уравнения, может вызвать неожиданные расхождения в результирующем изображении, при попытке достижения наилучшей подгонки всех исходных контрольных точек к конечным. Возможно, в этом примере, использование преобразования 3-го порядка было излишним, потому что порядок результирующих пикселей отличается от порядка входных пикселей по оси X (4 точка встала на 3 место, 3 оказалась на 4 месте).
Исходная координата X |
Конечная координата X |
|---|---|
1 |
x(1) = 17 |
2 |
x(2) = 7 |
3 |
x(3) = 1 |
4 |
x(4) = 5 |
x(1) > x(2) > x(4) > x(3)

В этом случае преобразование более высокого порядка, возможно, не даст ожидаемого результата, изображение будет сильно искажено.
Минимальное количество контрольных точек
Преобразования высших порядков могут быть использованы для корректировки очень сложных типов искажений. Однако для использования преобразований высших порядков требуется большее количество контрольных точек. Например, плоскость определяется 3-мя точками. Т.о. для применения преобразования 1-го порядка, которое выражается через уравнение плоскости, требуется как минимум 3 точки. Таким же образом, преобразование 2-го порядка выражается уравнением параболоида. Для определения уравнения параболоида требуется 6 точек. Поэтому, как минимум 6 контрольных точек требуется для осуществления преобразования 2-го порядка. Минимально требуемое количество точек для преобразования t-го порядка вычисляется следующим образом:
![]()
Использование количества контрольных точек больше минимального также возможно. Хотя, возможно, это даст лучшую подгонку, зачастую увеличение количества точек не имеет значения.
В следующей таблице перечислено минимальное количество контрольных точек необходимое для преобразований порядков с 1-го по 10-й.
Порядок преобразования |
Минимальное количество контрольных точек |
|---|---|
1 |
3 |
2 |
6 |
3 |
10 |
4 |
15 |
5 |
21 |
6 |
28 |
7 |
36 |
8 |
45 |
9 |
55 |
10 |
66 |
В статье использованы материалы ERDAS IMAGINE Field Guide
Обсудить в форуме Комментариев — 0
Ссылки по теме
Последнее обновление: September 09 2021
Дата создания: 19.02.2007
Автор(ы): Максим Дубинин
© GIS-Lab и авторы, 2002-2021. При использовании материалов сайта, ссылка на GIS-Lab и авторов обязательна. Содержание материалов - ответственность авторов. (подробнее).


