• Главная
• Вопросы и ответы

Использование метрики Левенштейна для поиска аналогов названий

Описание алгоритма и скрипт

Обсудить в форуме Комментариев — 4

Оглавление

1. Введение
2. Теория
3. Программная реализация

1. Введение

Расстояние Левенштейна (также редакционное расстояние или дистанция редактирования) — мера разницы двух строк относительно минимального количества операций вставки, удаления и замены, необходимых для перевода одной строки в другую или другими словами расстояние между строками.

В данной статье вводится понятие метрики, заданной на множестве строк и приводится пример функции, написанной на языке Python, вычисляющей расстояние между двумя строками.

Часто приходится иметь дело с информацией, представимой в виде последовательности символов, чисел и т.п., т.е. строковыми данными. При этом не менее часто в строковую информацию вносятся искажения, избежать которых очень трудно. Простейшим примером может служить любая более менее крупная база данных: почти навеняка в ней содержатся ошибки оператора, сделанные при наборе. Поэтому задача сравнения строк, определение степени их близости между собой, - задача весьма востребованная.

Практическая задача может быть представлена следующим образом. Имеем два набора данных, в нашем случае исходный - список названий населенных пунктов к которым нужно найти альтернативы, опорный - список правильных названий населенных пунктов. Исходный список может изобиловать ошибками и неточностями, необходимо посчитать расстояние от каждого вхождения исходного списка к опорным. Результат 0 может показывать, что в исходном списке есть абсолютный аналог в опорном, 1, что в опорном есть аналоги отличающиеся на 1 символ и т.д.

Метрика Левеншейна использовалась для перевода базы данных по населенным пунктам с Vmap0 на русский язык. В качестве опорной использовалась база данных КЛАДР.

2. Теория

Предположим, что имеется некоторое множество каких-либо элементов (например, множество символьных строк, или множество точек на плоскости или др.). Предположим, что было выбрано наугад два элемента заданного множества, и перед нами стоит задача установить, насколько они близки друг к другу. Если элементы заданного множества - точки евклидова пространства, то все решается просто: зная координаты точек, мы всегда можем определить расстояние между ними. А если множество состоит из более сложных объектов, у которых нет координат (как, например, строки)? Таким образом мы приходим к необходимости создания инструмента, позволяющего измерять расстояния между элементами множества. Таким инструментом является метрика - математическое обобщение понятия "расстояние".

Метрика - это фунция , которая берет на входе два элемента x и y исходного множества, и возвращает расстояние между этими элементами. Однако, функция - это не любая функция, а удовлетворяющая определенным условиям:

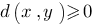1. для любых пар x и y, причем 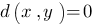тогда и только тогда, когда x=y. Требование очевидно: расстояние между объектами не может быть меньше нуля, и расстояние между совпадающими объектами должно быть равно нулю.
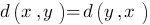2. для любых x и y. Также очевидное требование: расстояние не должно зависеть от того, как мы его меряем от x к y или в обратном направлении, от y к x.
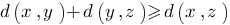3. . Это неравенство должно выполняться для любых x,y и z. Суть этого неравенства также понятна: путь "напрямую" должен быть короче (во всяком случае, не длиннее), чем "в объезд".

Эти три условия называются аксиомами метрики, а множество, на котором задана функция , удовлетворяющая этим аксиомам - метрическим пространством.

Понятно, что на одном и том же множестве можно задать разные метрики и в результате будут получаться разные пространства. При этом, может оказаться так, что при одном выборе метрики , а при другом выборе для этих же точек будет выполняться противоположное неравенство: . Поэтому при решении конкретной задачи, возможно, потребуется длительный процесс построения адекватной метрики.

На множестве строк может быть задано большое число метрик, соответствующих той или иной задаче. Здесь рассмотрим одну из такого рода метрик, называемую метрикой Левенштейна. Эту метрику применяют обычно для определения степени искажения строк. Мы не будем давать строгого определения метрики Левенштейна, лишь заметим, что, говоря простым языком, эта метрика представляет собой число опечаток, которые были сделаны при наборе строки test по сравнению с эталоном pattern. Например:

test	pattern	d(test,pattern)
abcd	acd	1
abcd1	abcd5	1
bcd	acd	1
axyd	acd	2
acbd	abcd	2
xyz	abcd	4

3. Программная реализация

• Python
• Pascal и внешняя dll

Python

Для решения конкретной задачи можно использовать следующую программную реализацию на языке Питон.

Работа производится с файлами dbf. Для работы необходим скрипт dbfpy. Перед запуском программы необходимо установить dbfpy.

Для работы необходимо:

1. Скачать и распаковать программный код
2. Установить парамеры в файле config.conf. Необходимо установить:
   • имя исходного файла - для которого надо произвести поиск: inFile и название поля в нем
   • имя рефенц-файла - является источником альтернатив: alternativeFile и название поля в нем inField
   • имя выходного файла - будет являться копией исходного + добавленные поля с результатом: newFile - имя файла, newStringField - имя строкового поля и максимальное число символов в этом поле (maxStrLen) и, наконец, newNumField - имя поля, в котором будут храниться полученные в результате работы скрипта расстояния до найденных альтернатив
   • настройки поиска: maxDist - максимально допустимое расстояние между шаблоном и альтернативой, levelCount - число уровней поискового дерева
3. Запустить скрипт поиска альтернатив conv.py при этом автоматически будет создано дерево поиска, определяемое в модуле searchtree.py. Поисковое дерево ускоряет процесс поиска альтернатив. При настройке числа уровней дерева нужно учитывать два противоположных требования: с одной стороны, чем больше уровней дерева будет построено, тем быстрее будет идти поиск альтернатив на больших файлах, с другой стороны, чем больше уровней будет задано, тем дольше будет строиться дерево.

Пример результата можно посмотреть в файле out1-sample.dbf

Pascal и внешняя DLL

Скачать исходный код на Pascal, DLL и скрипт на Avenue для использования библиотеки в Arcview GIS. Функция check принимает два строковых параметры и выдает целое число - результат.

Обсудить в форуме Комментариев — 4

Последнее обновление: September 09 2021

Дата создания: 09.09.2009
Автор(ы): Дмитрий Колесов, Максим Дубинин