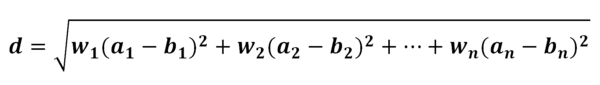Плагин Attribute based clustering - простая кластеризация векторных объектов по атрибутам в QGIS
Обсудить в форуме Комментариев — 1Редактировать в вики
по адресу http://gis-lab.info/qa/qgis-attr-based-clust.html
Кластеризация векторных объектов по атрибутам в QGIS: описание плагина для QGIS, используемые принципы, примеры использования
В географических исследованиях часто возникает задача типологии изучаемых объектов по набору формализованных параметров. Как сгруппировать большое количество объектов в небольшое число классов по совокупности показателей, определенных для каждого их этих объектов? Существуют различные подходы, в том числе и математический. В статье приводится краткое описание простого метода взвешенной иерархической кластеризации, а также упоминается классический K-Means; описывается разработанный плагин Attribute based clustering, реализующий их; приводится пример использования.
Кластеризация объектов[править]
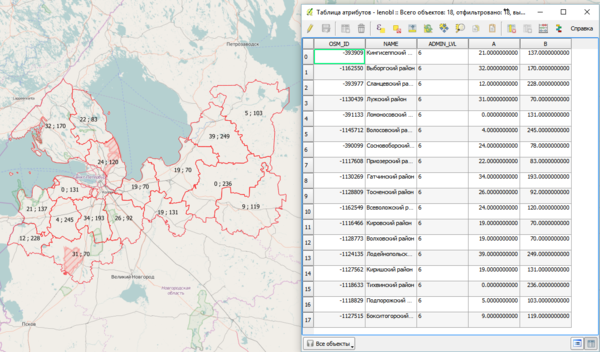
Обыкновенно, говоря о кластеризации объектов в ГИС, подразумевают их группировку по пространственному положению (для QGIS см. ConcaveHull Plugin, SciPy Clustering). Однако не менее интересной является кластеризация по атрибутам, когда пространственное положение объекта не играет роли (только если оно не формализовано как атрибут), а значимыми являются его некоторые числовые характеристики. Представьте себе, что каждый объект некоторого набора данных о районах Ленинградской области описывается двумя значениями A и B (это может быть что угодно - площадь, показатель престижности или конфликтогенности, количество музеев, средняя концентрация какого-либо вещества в атмосфере и пр. В данном случае значения получены случайным образом).
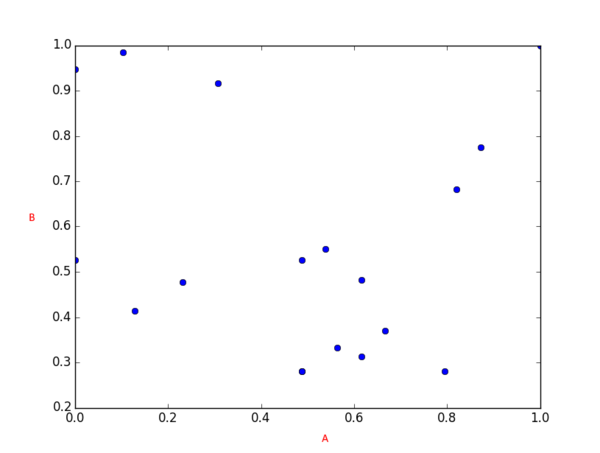
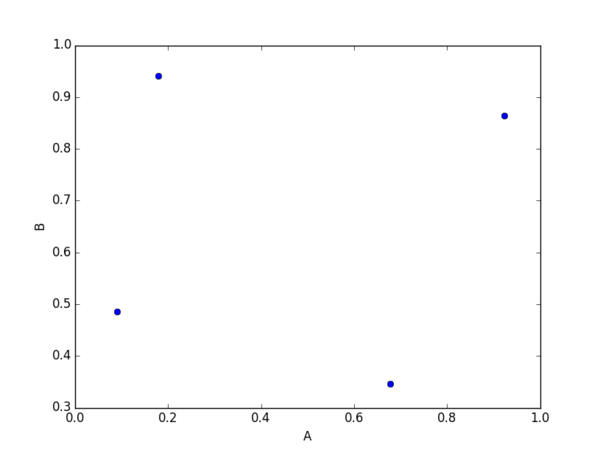
Поскольку пространственное положение нас не очень интересует, посмотрим на те же самые объекты в двумерном пространстве, где осями координат являются эти самые показатели A и B:
В данном случае, поскольку показатели неоднородны (т.е. у них разная метрика, условно, в A - экологический показатель, в B - показатель, связанный с людьми), для того, чтобы их можно было сравнивать, они были нормализованы (максимальное значение каждого показателя принято за 1, остальные изменены пропорционально). Именно поэтому на осях графика приведены не абсолютные значения A и B. Нормализация - не обязательная процедура, но она обеспечивает относительно равный вклад каждого показателя в кластеризацию, вне зависимости от их метрики. Иногда, если, к примеру, кластеризация осуществляется по некоторым "балльным" показателям, уже приведенным в нужную исследователю шкалу, нормализация может и навредить.
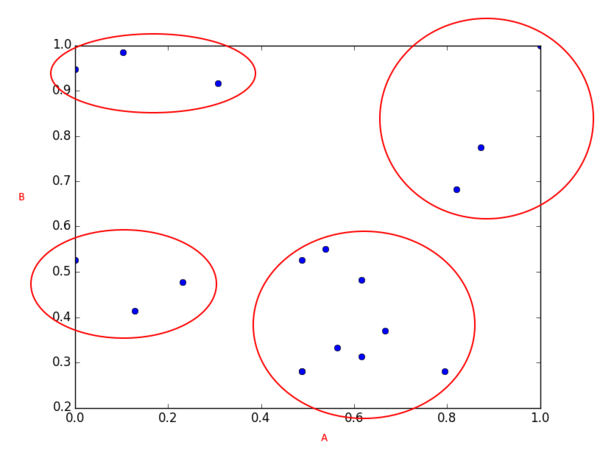
Возвращаясь к полученному графику, зададимся целью выделить четыре категории и отнести каждый объект к одной из них, основываясь на их близости в таком двумерном пространстве признаков A - B. В данном случае визуально легко выделяются четыре группы.
Присвоив соответствующим районам номера групп, в которые они попали, мы решим задачу кластеризации. Однако, развивая мысль, можно столкнуться с массой усложнений: если объектов будет гораздо больше, и группы не будут выделяться так явно - как быть? А что, если производить группировку не по двум показателям, а по N (в N-мерном пространстве признаков)? Да и желаемое количество кластеров может быть очень различным. Визуальной оценкой графика уже не обойдешься!
Взвешенная иерархическая кластеризация[править]
Самый простой, но понятный с точки зрения логики работы алгоритм - иерархическая кластеризация. Его сущность заключается в последовательном объединении наиболее близких друг к другу объектов в группы до тех пор, пока таких групп не останется ровно столько, сколько требуется выделить кластеров. Опишем принцип на примере тех же самых районов Ленинградской области. Первый шаг - считаем каждый отдельный объект принадлежащим своей собственной, независимой группе (в нашем случае начинаем с 18 групп). Вычисляем расстояния между всеми этими группами и... Так, а вот только что считать расстоянием? Самый простой способ - расстояние в N-мерном евклидовом пространстве, вычисляемое по формуле:
где d - собственно расстояние; an, bn - координаты объектов a и b на n-ой оси пространства; wn - вес n-го признака.
Вес здесь - некоторое необязательное дополнение. Вводится для того, чтобы у исследователя была возможность регулировать вклад каждого конкретного параметра в расчёты. Чем меньше вес - тем меньшим выходит вклад n-ого признака в результирующее расстояние.
Результатом расчёта по такой формуле (в данном случае с равными весами = 1) является матрица расстояний (для оптимизации использования ресурсов - только одна её половина, вторая была бы симметричной). В нашем случае она выглядит вот так:
[[0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], [0.31, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], [0.43, 0.56, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], [0.37, 0.40, 0.80, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], [0.54, 0.84, 0.50, 0.83, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], [0.61, 0.78, 0.22, 0.99, 0.47, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], [0.25, 0.42, 0.68, 0.18, 0.65, 0.84, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], [0.22, 0.43, 0.64, 0.24, 0.60, 0.80, 0.06, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], [0.40, 0.11, 0.58, 0.50, 0.91, 0.80, 0.53, 0.54, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], [0.22, 0.35, 0.65, 0.16, 0.68, 0.83, 0.08, 0.11, 0.45, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], [0.10, 0.29, 0.53, 0.27, 0.62, 0.72, 0.17, 0.16, 0.39, 0.12, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], [0.27, 0.52, 0.66, 0.31, 0.55, 0.80, 0.13, 0.09, 0.63, 0.20, 0.24, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], [0.27, 0.52, 0.66, 0.31, 0.55, 0.80, 0.13, 0.09, 0.63, 0.20, 0.24, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00], [0.64, 0.36, 0.70, 0.75, 1.11, 0.90, 0.79, 0.80, 0.26, 0.71, 0.65, 0.88, 0.88, 0.00, 0.00, 0.00, 0.00, 0.00], [0.06, 0.37, 0.43, 0.39, 0.49, 0.60, 0.25, 0.21, 0.46, 0.24, 0.14, 0.24, 0.24, 0.70, 0.00, 0.00, 0.00, 0.00], [0.67, 0.86, 0.31, 1.04, 0.42, 0.11, 0.88, 0.83, 0.89, 0.88, 0.77, 0.83, 0.83, 1.00, 0.64, 0.00, 0.00, 0.00], [0.43, 0.74, 0.53, 0.68, 0.17, 0.57, 0.50, 0.44, 0.83, 0.54, 0.49, 0.38, 0.38, 1.05, 0.38, 0.55, 0.00, 0.00], [0.32, 0.62, 0.44, 0.60, 0.24, 0.52, 0.42, 0.36, 0.71, 0.45, 0.38, 0.32, 0.32, 0.93, 0.26, 0.52, 0.12, 0.00]]
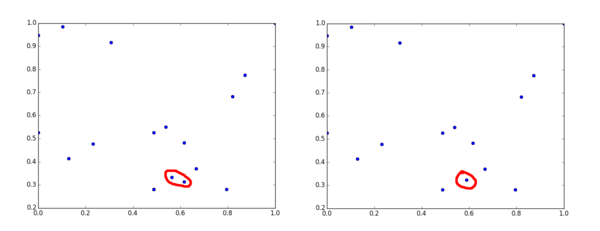
Теперь найдем в ней минимальное расстояние: 0.06. Оно соответствует двум объектам, которые находятся ближе всего друг к другу в нашем пространстве признаков (1 и 15). Объединяем их в одну группу, рассчитывая для этого их среднее положение. Теперь кластеров стало на один меньше: а две точки слились в одну. Посмотрим на график ещё раз:
Хорошо видно, что были объединены две самые близкие точки. Возвращаемся к расчёту расстояний (теперь новых, ведь ситуация изменилась) и построению матрицы. Её размерность, конечно, уменьшится на 1. Повторяем поиск минимального расстояния и объединение точек. Развлекаясь так некоторое время, обнаруживаем, что осталось всего 4 точки:
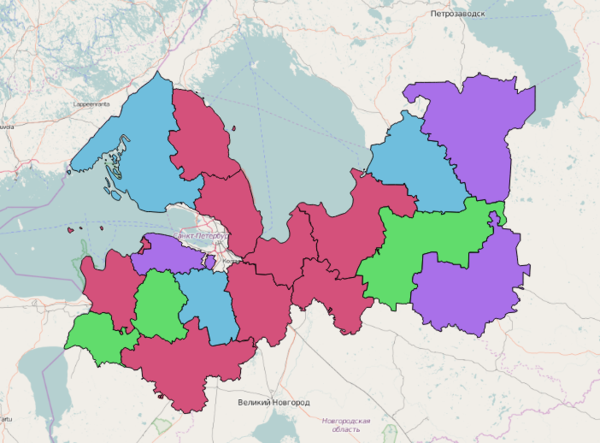
Это, по сути, центры искомых кластеров. Пометив, какая исходная точка попала в конечном итоге в какую из этих 4х, мы получаем список точек-участниц каждой группы. А это и есть искомое. Покрасив районы Ленинградской области в соответствии с принадлежностью к группам, визуализируем результаты кластеризации:
Алгоритм справится с практически любым количеством признаков (параметров), по которым исследователю нужно кластеризовать объекты, а возможность задавать веса делает его достаточно гибким. Но есть и существенный недостаток - необходимость расчёта матрицы расстояний (размером NxN, где N - текущее количество групп). Если ваш набор данных содержит 1000 объектов, матрица на первом этапе будет содержать 1000000 ячеек, из которых для ~500000 придётся рассчитывать расстояния (при минимальной оптимизации). При работе с разработанным модулем, реализующим иерархический метод, как будет показано дальше, относительно комфортно можно обрабатывать слои с сотнями и первыми тысячами объектов. Основным преимуществом, на взгляд автора статьи, является максимальная понятность и естественность происходящего в методе, его простота.
K-Means[править]
K-Means - классический метод, широко описанный в литературе и статьях в сети Интернет. Общая идея заключается в следующем: изначально выбираются N (по числу требуемых групп) центров, которые затем итеративно перевычисляются таким образом, чтобы минимизировать суммарное квадратичное отклонение точек, относимых к этим центрам [wikipedia]. Существующие реализации (для модуля использована scipy.cluster) обеспечивают очень быструю обработку больших наборов данных, однако у быстродействия есть своя цена - нестабильность, обусловленная сильной зависимостью от начального выбора кластеров (в данном случае случайного). Компенсировать эту нестабильность можно лишь увеличивая число итераций перевычисления центров кластеров, что, очевидно, негативно сказывается на той же производительности. При работе с большими массивами данных, когда иерархическая кластеризация требует слишком много ресурсов, K-Means выручает и демонстрирует хорошие результаты. Помимо нестабильности, среди недостатков можно упомянуть, что в scipy-реализации нет поддержки весов.
Плагин Attribute based clustering[править]
Общая информация[править]
Разработанный модуль реализует кластеризацию по атрибутам вышеописанными методами. Иерархическая кластеризация нативная и не требует дополнительных библиотек, K-Means требует наличия SciPy. Распространяется по лицензии GNU GPL v2, поддерживается версиями QGIS от 2.0 и выше.
Для установки модуля достаточно загрузить архив и распаковать его содержимое как директорию в <home dir>/.qgis2/python/plugins/
Например, в Windows это может быть папка C:/users/silent/.qgis2/python/plugins/attributeBasedClustering/
В Linux: /home/silent/.qgis2/python/plugins/attributeBasedClustering/
Описание[править]
Основным результатом работы модуля является создание нового (или перезапись существующего) атрибута векторного слоя с записью в него для каждого объекта номера кластера, к которому объект оказался отнесён в результате расчётов. Пользователь выбирает исследуемый векторный слой, задаёт атрибуты (числовые), которые будут использоваться как признаки при кластеризации, при необходимости задаёт им веса, выбирает метод кластеризации, количество кластеров, имя атрибута для записи результатов, а также устанавливает или снимает флаг, обозначающий необходимость нормализации значений атрибутов. Поддерживаются два алгоритма кластеризации:
- K-Means (не взвешенная, сторонняя реализация (scipy), быстрая)
- Иерархическая (взвешенная, нативная реализация, медленная)
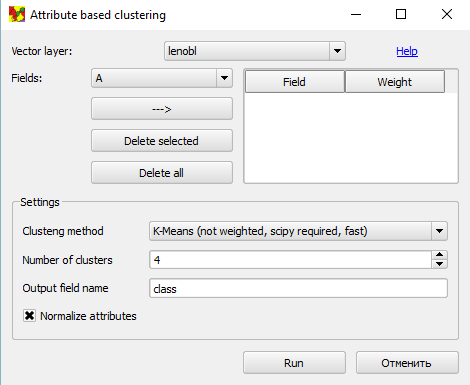
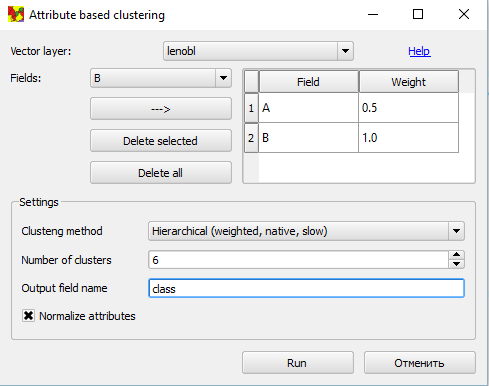
Интерфейс очень прост:
Определив слой, пользователь, поочередно выбирая атрибуты и нажимая кнопку "--->" добавляет их в таблицу. Добавленные атрибуты можно удалять, а также задавать для них веса (для иерархической кластеризации). На изображении ниже атрибуты A и B слоя районов Ленинградской области выбраны как признаки кластеризации, причем вес атрибута A уменьшен до 0.5. Выбрана иерархическая кластеризация, цель - 6 классов, используется нормализация значений.
Использование[править]
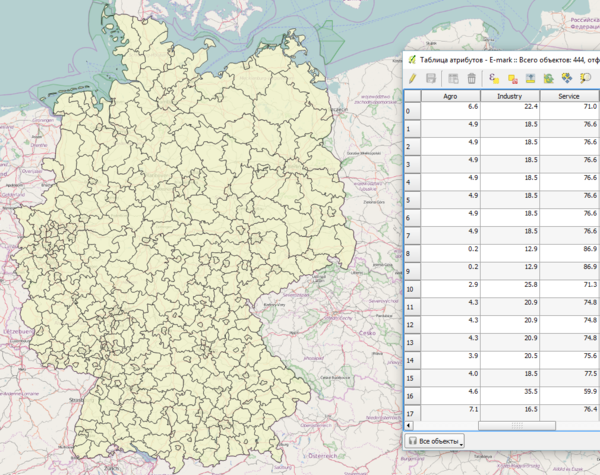
В качестве примера использования приведём кластеризацию районов Германии по социально-экономическим показателям.
Для этого используем слой, собранный из открытых источников (автор - Анна Иванова), содержащий районы (444 объекта) Германии с параметрами, определяющими развитие сельского хозяйства, промышленности и сферы обслуживания в каждом конкретном районе.
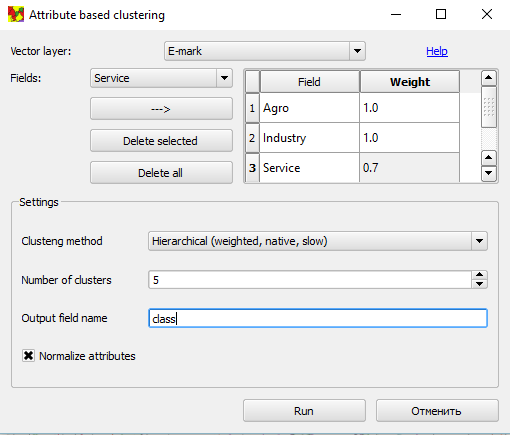
Используя алгоритм иерархической кластеризации, выделим пять типов районов по этим трём показателям, причём сфера обслуживания нам интересна несколько в меньшей степени, чем другие признаки. Задаём соответствующие параметры:
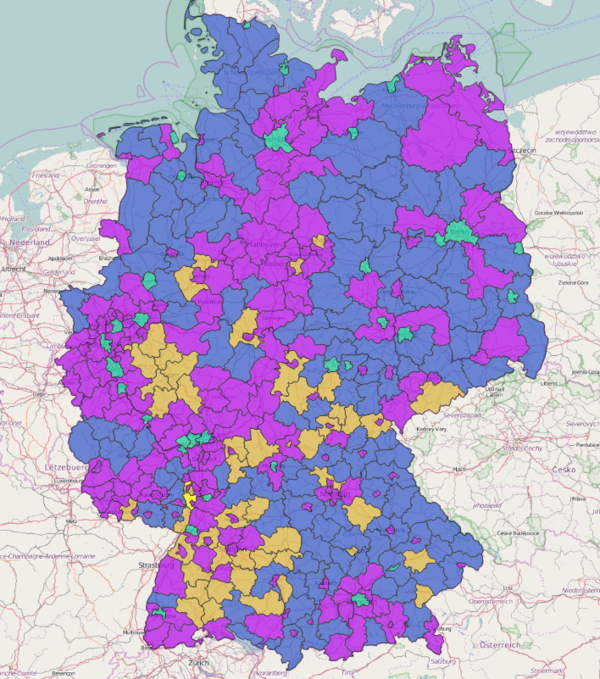
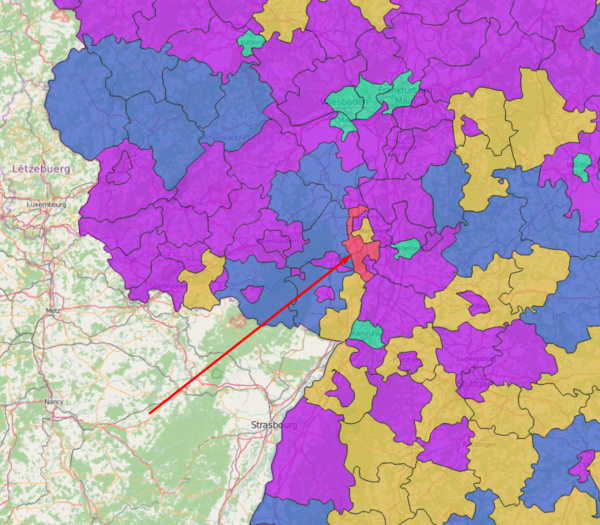
Результат работы - новый атрибут в слое, содержащий номер кластера для каждого объекта. Настроив стиль, получим карту типизации районов Германии на 5 категорий:
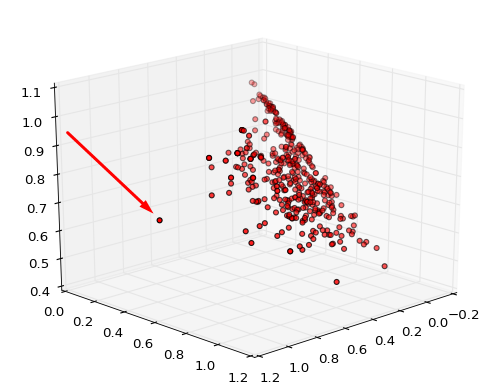
Внимательно изучив получившуюся карту, можно обнаружить, что в один из кластеров попал только один объект. Похоже на ошибку?
Однако если посмотреть на 3х-мерное (ведь мы использовали три атрибута) пространство признаков, увидим, что этот одинокий объект и правда прилично отстоит от остальных:
и алгоритм кластеризации всё сделал разумно. В целом, эти простые подходы к выделению типов объектов могут помочь вам в разнообразных исследованиях для поверхностной и быстрой оценки тех или иных процессов.
Обсудить в форуме Комментариев — 1Редактировать в вики
Последнее обновление: 2016-05-20 21:40
Дата создания:
Автор(ы): Эдуард Казаков
© GIS-Lab и авторы, 2002-2021. При использовании материалов сайта, ссылка на GIS-Lab и авторов обязательна. Содержание материалов - ответственность авторов. (подробнее).