Пересчет координат из Lat/Long в проекцию Меркатора и обратно
Описаны формул пересчета широты/долготы в плоские координаты по проекции Меркатора на сфере по версии Google Maps и на эллипсойде WGS84.
Обсудить в форуме Комментариев — 147
Картографический веб-сервис Google Maps для отображения карт использует проекцию Меркатора на сфере. Для начала рассмотрим более общий случай проекции Меркатора для эллипсоида WGS84, а потом будет не сложно перейти к сфере.
Содержание
- Пересчет координат из широты/долготы в проекцию Меркатора
- Проверка результатов
- Пересчет координат из проекции Меркатора в широту/долготу
- Реализации пересчетов
Описание проекции Меркатора более подробно можно посмотреть в следующих источниках:
Пересчет с помощью библиотеки PROJ.4:
В процессе пересчета понадобятся также следующие параметры:
- Ложный сдвиг на восток False Eastings = 0
- Ложный сдвиг на север False Northings = 0
- Масштабный коэффициент Scale Factor = 1
- Большая полуось эллипсоида WGS84: a = 6378137.0 м
- Малая полуось эллипсоида WGS84: b = 6356752.3142 м
- Сфера используемая в Arcview GIS: a=b=6370997
Пример:
Будем использовать для примера координаты г. Москва: 55.751667 с.ш., 37.617778 в.д.
Пересчет координат из широты/долготы в проекцию Меркатора
Основные формулы:
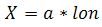
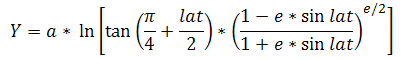
где:
- lon/lat - долгота/широта в радианах;
- e - эксцентриситет эллипса;
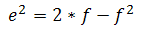
- где: f - коэффициент уплощения Земли
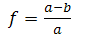
- или выразив эксцентриситет через полуоси:
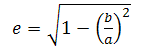
- где: f - коэффициент уплощения Земли
Пересчет в R:
Lat=55.751667 Long=37.617778 rLat=Lat*pi/180 rLong=Long*pi/180 a=6378137 b=6356752.3142 f=(a-b)/a e=sqrt(2*f-f^2) X=a*rLong Y=a*log(tan(pi/4+rLat/2)*((1-e*sin(rLat))/(1+e*sin(rLat)))^(e/2)) X [1] 4187592 Y [1] 7473789
Пересчет в Proj.4:
proj +proj=merc +ellps=WGS84 37.617778 55.751667 4187591.89 7473789.46
Для пересчета на сферу:
proj +proj=merc +ellps=sphere 37.617778 55.751667 4182904.10 7500731.48
Скачать пример пересчета координат из Lat/Long в Mercator на сфере и эллипсоиде WGS84 (Excel).
X = 4182904.096
Y = 7500731.483
Проверка результатов
lat = 55.751667, long = 37.617778
| Arcview GIS | Proj | Excel | |
| WGS84 | 7473789.46 4187592.00 | 7473789.46 4187591.89 | 7473789.462 4187591.892 |
| Сфера | 7500731.48 4182904.10 | 4182904.10 7500731.48 | 7500731.483 4182904.096 |
Пересчет координат из проекции Мекартора в широту/долготу
Основные формулы:
![]()
Широта вычисляется методом приближения в цикле:
Расчитаем для примера координаты нашего проверочного пункта в географической системе координат WGS 84, используя как исходные координаты из предыдущего примера:
Y=7473789
X=4187592
a=6378137
b=6356752.314
f=(a-b)/a
e=sqrt(2*f-f^2)
eh=e/2
pih=pi/2
ts=exp(-Y/a)
phi=pih-2*atan(ts)
i=0
dphi=1
while () {
con=e*sin(phi)
dphi=pih-2*atan(ts*((1-con)/(1+con))^e))-phi
phi=phi+dphi
}
rLong=X/a
rLat=phi
Long=rLong*180/pi
Lat=rLat*180/pi
Реализации пересчетов
Реализация пересчета на языке C++ (Источник: Proj.4, PJ_merc.c). Реализации на языках Java, Python, C# и др. для направления DD->Mercator доступны в Вики Openstreetmap.
private static const PI_2:Number = Math.PI * 0.5;
private static const MAX_LAT:Number = 89.5;
private static const R_MAJOR:Number = 6378137.0;
private static const R_MINOR:Number = 6356752.3142;
private static const ECCENT:Number = Math.sqrt(1 - Math.pow(R_MINOR / R_MAJOR, 2));
private static const ECCNTH:Number = ECCENT * 0.5;
public static function merc_x(longitude:Number):Number
{
return longitude * DEG_RAD * R_MAJOR;
}
public static function unmerc_x(longitude:Number):Number
{
return longitude * RAD_DEG / R_MAJOR;
}
public static function merc_y(latitude:Number):Number
{
if (latitude > MAX_LAT) latitude = MAX_LAT;
if (latitude < -MAX_LAT) latitude = -MAX_LAT;
var phi:Number = latitude * DEG_RAD;
var con:Number = ECCENT * Math.sin(phi);
con = Math.pow( (1.0 - con) / (1.0 + con), ECCNTH );
return -R_MAJOR * Math.log( Math.tan(0.5 * (PI_2 - phi)) / con );
}
public static function unmerc_y(y:Number):Number
{
var ts:Number = Math.exp(-y / R_MAJOR);
var phi:Number = PI_2 - 2.0 * Math.atan(ts);
var i:uint = 0;
var dPhi:Number = 1;
while( (dPhi >= 0 ? dPhi : -dPhi) > 0.000000001 && i++ < 15 )
{
var con:Number = ECCENT * Math.sin(phi);
dPhi = PI_2 - 2.0 * Math.atan (ts * Math.pow((1.0 - con) /
(1.0 + con), ECCNTH)) - phi;
phi += dPhi;
}
return phi * RAD_DEG;
}
Обсудить в форуме Комментариев — 5
Ссылки по теме
Последнее обновление: September 09 2021
© GIS-Lab и авторы, 2002-2021. При использовании материалов сайта, ссылка на GIS-Lab и авторов обязательна. Содержание материалов - ответственность авторов. (подробнее).


