Страница 1 из 2
Проекции скоростей в системах координат
Добавлено: 19 окт 2018, 12:42
chiroptera
Добрый день!
Возникла необходимость перевода проекций скорости в проекции Гаусса-Крюгера в геоцентрическую систему координат. Т.е. по сути нужна матрица поворота для перехода от одной системы координат в другую.
В ГОСТе Р 51794-2008 отлично описаны преобразования пространственных координат из одной системы в другую. Как мне видится, имея вектор скорости в локальной проекции Гаусса-Крюгера, но с добавлением оси Z, с помощью матрицы поворота относительно известной заданной точки можно получить вектор скорости, так же разложенный по осям, уже в геоцентрической системе координат.
Удалось найти информацию, что матрица поворота будет такой:
-sinL -sinB*cosL cosL*cosB
cosL -sinB*sinL sinL*cosB
0 cosB sinB
Но L и B - это же долгота и широта в геодезической системе координат, получается какое-то скидывание всего в общую кучу... При моделировании, конечно же, результаты получается далекими от ожидаемых.
Так же не удалось найти никаких выводов, почему матрица поворота именно такая.
Просьба посоветовать, что еще можно прочитать на данную тему (грамотный запрос к гуглу уже не знаю, как сделать, чтобы найти не кучу бреда и по сто раз переписанных формул без обоснований), или какие подсказки, если кто-то сталкивался с похожей задачей
Re: Проекции скоростей в системах координат
Добавлено: 19 окт 2018, 13:12
trir
Re: Проекции скоростей в системах координат
Добавлено: 19 окт 2018, 14:27
Игорь Белов
Вектор скорости редуцирован на плоскость в проекции и нужна геодезическая точность? Мне видится такой двухступенчатый алгоритм:
- переход из проекции в топоцентрическую СК;
- из топоцентрической в геоцентрическую.
На первом этапе по положению в проекции X, Y вычисляем геодезические широту и долготу B, L.
Также с помощью масштаба отображения m и сближения меридианов γ из скорости в проекции v и дирекционного угла α получаем скорость V и азимут A:
V = v / m
A = α + γ
m ≈ 1 + y² / 2 R² + y⁴ / 24 R⁴
tg γ ≈ tg (L − L₀) sin B
Здесь y = Y − Y₀ — разность восточной координаты и её значения на осевом меридиане (внимание, тут геодезический Y; в геодезии X направлен на север, Y на восток); L − L₀ — разность геодезической долготы и долготы осевого меридиана. R — средний радиус кривизны эллипсоида в точке
R = c / (1 + e′² cos² B)
Не знаю точностных требований в Вашей задаче. Возможно, достаточно принять R ≈ 6371000 м.
Всё необходимое для второго этапа есть в статье
Геодезические системы пространственных координат
P. S. Если вектор скорости действительно был редуцирован на плоскость в проекции (в чём лично я сомневаюсь), придётся отслоить его от эллипсоида и перенести обратно на высоту точки H:
v = v_редуц (R + H) / R
P. P. S. Если скорость измерена на наклонной поверхности, нужно это учесть. Компоненты скорости в топоцентрической системе координат:
Vx = V cos η cos A
Vy = V cos η sin A
Vz = V sin η
Здесь η — угол возвышения траектории (уклона дороги?).
Re: Проекции скоростей в системах координат
Добавлено: 19 окт 2018, 15:44
chiroptera
Игорь Белов писал(а): ↑19 окт 2018, 14:27
Вектор скорости редуцирован на плоскость в проекции и нужна геодезическая точность?
Игорь Белов писал(а): ↑19 окт 2018, 14:27
Если вектор скорости действительно был редуцирован на плоскость в проекции (в чём лично я сомневаюсь), придётся отслоить его от эллипсоида и перенести обратно на высоту точки H
Все верно, вектор не был редуцирован на плоскость и рассчитан исключительно как проекция на оси. Предполагается, что он и находится на некоторой высоте. Т.е. точность не требует рассмотрения конкретных эллипсоидов, как я понимаю, в терминологии это равнозначно квазигеоиду, Поправьте, если ошибаюсь.
Координаты перемещающейся точки известны в геоцентрической и геодезической системах, а также в Г-К.
Re: Проекции скоростей в системах координат
Добавлено: 20 окт 2018, 18:37
Игорь Белов
Не знаю порядка координат, предположу направление осей X на восток, Y на север, как в САПР/ГИС. Дополним вектор скорости v третьей компонентой vz = 0.
Если скорости измеряются с точностью не выше 1/1000, а положения не выходят за пределы шестиградусной зоны, можно принять масштаб отображения m равным единице. Но от сближения меридианов избавиться не удастся, поэтому первое элементарное вращение должно быть связано с ним. Соответствующая матрица вращения вокруг оси Z на угол γ − 90° Rz(γ − 90°). Теперь вектор скорости определён в топоцентрической системе координат, где оси X, Y, Z направлены соответственно на юг, на восток, вверх.
Далее, как предлагается в статье, последовательно вращаем вокруг оси Y на угол B − 90° и вогруг оси Z на угол −L.
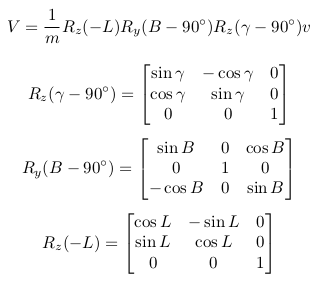
- Screenshot_2018-10-20_17-47-05.png (14.8 КБ) 11194 просмотра
где v — исходный вектор скорости, дополненный нулевой вертикальной компонентой, V — вектор скорости в геоцентрической системе координат, m — масштаб отображения в проекции, γ — сближение меридианов, B — широта, L — долгота.
Не вижу большого смысла в явном вычислении общей матрицы вращения, — она выгодна, когда положение неизменно. Но если нужна, получим её, последовательно перемножив матрицы элементарных вращений:
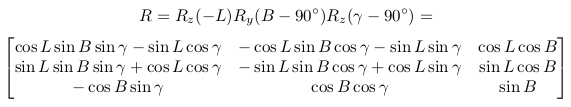
- Screenshot_2018-10-20_17-47-06.png (3.97 КБ) 11194 просмотра
Если же порядок координат как у геодезистов, X на север, Y на восток, нужно преобразовать левую координатную систему в правую. Предлагаю изменять знак первой компоненты vx на обратный:
vx′ = −vx
vy′ = vy
vz′ = 0
Первое вращение будет вокруг оси Z на угол γ. В приведённых матрицах вращения достаточно сделать замены
cos γ ⇒ sin γ
sin γ ⇒ −cos γ
Re: Проекции скоростей в системах координат
Добавлено: 20 ноя 2018, 11:31
chiroptera
Хотелось бы прояснить момент с направлением координатных осей. Проекция Гаусса-Крюгера представляет собой лепесток, из стандарта ось Х направлена на север, ось Y на восток. Это не априори? Т.е. в САПР/ГИС идёт разворот осей?
Геоцентрическая система координат представляет собой декартову систему координат.
Соответственно, я понимаю, что от угла сближения меридианов избавиться не получится, но остаётся вращение вокруг оси Х, Не понимаю, почему вокруг оси Z есть второй вращение на угол -L.
Извиняюсь за вопросы, занимаюсь другой сферой, но возникла необходимость получить знания в геодезии.
Re: Проекции скоростей в системах координат
Добавлено: 20 ноя 2018, 11:37
trir
из стандарта ось Х направлена на север, ось Y на восток. Это не априори? Т.е. в САПР/ГИС идёт разворот осей?
считаем, что X это Y, а Y это X

Не понимаю, почему вокруг оси Z есть второй вращение на угол -L.
ось Z направленна на север
Re: Проекции скоростей в системах координат
Добавлено: 20 ноя 2018, 12:15
chiroptera
trir писал(а): ↑20 ноя 2018, 11:37
считаем, что X это Y, а Y это X
Так написать - самое простое

Есть какое-то обоснование, почему вдруг произошёл такой разворот?
Не могу сформулировать адекватно, что смущает

Я понимаю, что для Вас это просто. Попробую так: в декартовой системе координат три оси. Изначально в проекции Гаусса-Крюгера только две, дополняем систему координат третью осью Z, чтобы учитывать высоту. В итоге получается сфера в декартовой системе координат (обзовем наш геоид сферой), на поверхности сферы есть некая точка Q0 (например), которая является нулём для другой декартовой системы координат (проекция, дополненная осью для высоты). Есть где-то ошибка в понимании?
Осей три, а поворот происходит только относительно Y и Z. Почему?
Далее в матлабе был написан простенький скрипт, в котором используется матрицы поворота R из коммента Игоря Белова. Сравниваю скорости, полученные расчётом и данные с GPS приёмника. Знаки проекции скорости совпадают, уже хорошо. Но убежали модули значений для y и z оставляющих вектора скорости
Как мне видится, ось Z поворачивается на угол 90-B, ось X - на 180-L. Далее ось Y сама встаёт на нужное место. Но в данном случае не учитывается сближение меридианов, а чем ближе к полюсам, тем сильнее их влияние
Re: Проекции скоростей в системах координат
Добавлено: 20 ноя 2018, 13:28
gamm
chiroptera писал(а): ↑20 ноя 2018, 12:15
Есть какое-то обоснование, почему вдруг произошёл такой разворот?
потому, что Easing, Northing Гаусса-Крюгера не имеют отношения к геоцентрической системе координат (и имеющимся там XYZ). У вас цилиндр (который в поперечном Меркаторе), и ось которого дает Easing, повернут вокруг оси Z геоцентрической системы на долготу. Нужно вернуть назад. Аналогично с Northing, там компенсируем кривизну цилиндра.
Re: Проекции скоростей в системах координат
Добавлено: 20 ноя 2018, 18:16
Игорь Белов
Во всём этом потоке сознания не хватает необходимого — постановки задачи. Что именно измеряется? Как измеряется? Каковы предполагаемые инструменты вычислений? Как результаты сравниваются с данными ГНСС-измерений и с какими именно данными?
Обидно терять время на задачу, вводные данные которой состоят из домыслов.
Re: Проекции скоростей в системах координат
Добавлено: 21 ноя 2018, 09:41
juffin_h
chiroptera писал(а): ↑19 окт 2018, 12:42
Т.е. по сути нужна матрица поворота для перехода от одной системы координат в другую.
С чего Вы взяли, что для перехода достаточно поворота? Что то Вы перемудрили.
chiroptera писал(а): ↑19 окт 2018, 12:42
Возникла необходимость перевода проекций скорости в проекции Гаусса-Крюгера в геоцентрическую систему координат.
Ну так и переводите плоские -> геодезические -> пространственные.
Re: Проекции скоростей в системах координат
Добавлено: 21 ноя 2018, 10:35
gamm
juffin_h писал(а): ↑21 ноя 2018, 09:41
Ну так и переводите плоские -> геодезические -> пространственные.
кстати, да: достаточно перевести два конца вектора штатными средствами PROJ

Re: Проекции скоростей в системах координат
Добавлено: 21 ноя 2018, 17:33
chiroptera
Есть вектор скорости в проекции Гаусса-Крюгера. Есть точка начала вектора. Нужно перевести вектор в геоцентрическую систему координат, не используя метод переноса по двум точкам.
Из ГОСТа легко строится цепочка Гаусса-Крюгера -> геодезическая система координат - > геоцентрическая система координат для конкретной точки. Собственно, написана рабочая модель, полученные значения во всех трех системах координат проверены по GPS данным.
Задача: перенести вектор из проекции Гаусса-Крюгера (вектор дополнен вертикальной составляющей) в геоцентрическую систему координат.
Re: Проекции скоростей в системах координат
Добавлено: 21 ноя 2018, 17:46
chiroptera
В матлабе есть функция enu2geodetic. В данном случае ENU и есть моя система Гаусса-Крюгера, которая была дополнена вертикальной составляющей.
Синтаксис:
Код: Выделить всё
[lat,lon,h] = enu2geodetic(xEast,yNorth,zUp,lat0,lon0,h0,spheroid)
xEast - координата Х в проекции Гаусса-Крюгера, число слева обязательно дополнено номером зоны (на лепестке X на север, Y на восток)
yNorth - координата Y в проекции Гаусса-Крюгера, число слева обязательно дополнено номером зоны
zUp - высота, на которой находится объект
spheroid - указываю WGS84
lat0, lon0 - широта и долгота какой точки?
Мне представляется, что начало вектора можно совместить с началом координат локальной системы. Тогда B, L соответствуют координатам начала вектора в геодезической системе координат. Но на выходе имею ерунду
Т.е. резюмируя, я могу перевести по формулам из ГОСТа точку из Гаусса-Крюгера в геодезическую систему. Не могу этого сделать через функцию в матлабе.
Очень хочется верить, что как только получится понять, где ошибка в этом месте, получится перевести и вектор по абсолютным значениям проекций на координатные оси
При этом успешно перевожу из геодезической в локальную (абстрактную) систему координат и далее в геоцентрическую. И обратно.
Re: Проекции скоростей в системах координат
Добавлено: 21 ноя 2018, 18:08
trir
В матлабе есть функция enu2geodetic. В данном случае ENU и есть моя система Гаусса-Крюгера, которая была дополнена вертикальной составляющей.
Гаусс-Крюгер там не причём