Это мысли вслух, собирался их проверить, но вот уже три дня, как руки не доходят -- понял, что экспериментально и не сделаю, но хотя бы напишу идею, может поможет.
В основе лежит идея кубических сплайнов -- когда каждом на интервале между точками (x_i, x_{i+1}) используется своя функция f_i для аппроксимации, в итоге сколько интервалов, столько и функций.
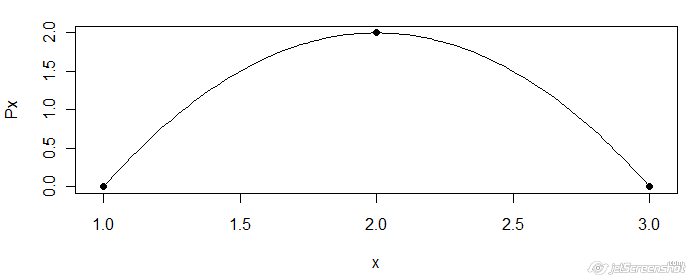
Рассмотрим пример с точками, заданными выше:
x = 1, 2, 2.5, 3
y = 0, 2, 0.5, 0
получаем три интервала и три функции f1, f2, f3. Далее на функции накладываются ограничения, которые рассмотрим на примере функции f2, заданной на интервале (2, 2.5).
- 1) Чтобы не было разрывов, естественно потребовать, чтобы значения соседних функций на границе отрезков совпадали f1(2) = f2(2) и f2(2.5)=f3(2.5). Получаем два условия на функцию f2.
2) Чтобы итоговая функция не выглядела "сломанной" на границах отрезков, нужно, чтобы производные этих функций также совпадали: f1'(2) = f2'(2) и f2'(2.5)=f3'(2.5). Так получаем еще два ограничения на на функцию f2.
Аналогичная картина и с функциями на других отрезках. Итого 4 ограничения, которым должна удовлетворять некоторая функция f. Если использовать при работе полиномы, то получается, что нам потребуется полином с четырьмя коэффициентами, чтобы можно было составить систему уравнений из 4-х условий. Отсюда вытекает, что каждую f_i следует искать в виде кубического полинома.
Итоговая функция F будет получена из набора функций f1, f2, f3,..., каждая из которых задана на своем отрезке.
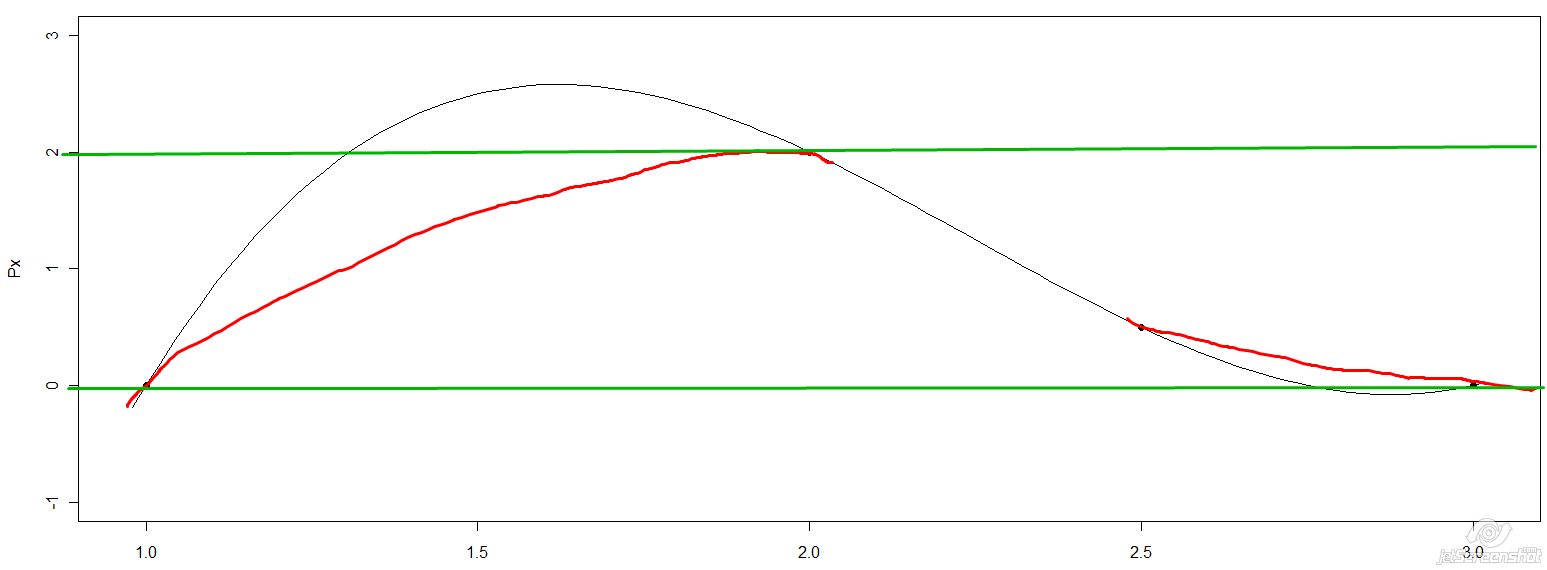
Теперь идем далее. Что в сплайнах нехорошо для условий данной задачи? А то, что в сплайнах нет места на дополнительные ограничения max(F) = M и min(F)=m -- все степени свободы уже заняты, контролировать максимумы и минимумы нечем.
Предлагаю попробовать отказаться от жестких равенств f_i(xi) = f_{i_1}(xi) и f_i'(xi) = f_{i_1}'(xi), а допустить небольшую погрешность. Тогда в точке xi можно составить невязку e1 = f_i(xi) - f_{i_1}(xi), e2 = f_i'(xi) = f_{i_1}'(xi). Далее суммируем квадраты невязок по всем точкам, получаем суммарные невязки E1 и E2.
Последний шаг: оптимизируем функцию W1 E1 + W2 E2 + W3 (max(F) - M)^2 + W4 (min(F) - m) относительно коэффициентов полиномов каким-либо методом оптимизации. Веса Wi отвечают за относительную важность каждого отдельного критерия и подбираются из каких-либо логических соображений или экспериментально.